Sampling with Shielded Langevin Monte Carlo Using Navigation Potentials

We introduce shielded Langevin Monte Carlo (LMC), a constrained sampler inspired by navigation functions, capable of sampling from unnormalized target distributions defined over punctured supports. In other words, this approach samples from non-convex spaces defined as convex sets with convex holes. This defines a novel and challenging problem in constrained sampling. To do so, the sampler incorporates a combination of a spatially adaptive temperature and a repulsive drift to ensure that samples remain within the feasible region. Experiments on a 2D Gaussian mixture and multiple-input multiple-output (MIMO) symbol detection showcase the advantages of the proposed shielded LMC in contrast to unconstrained cases.

Learning Globally Smooth Functions on Manifolds

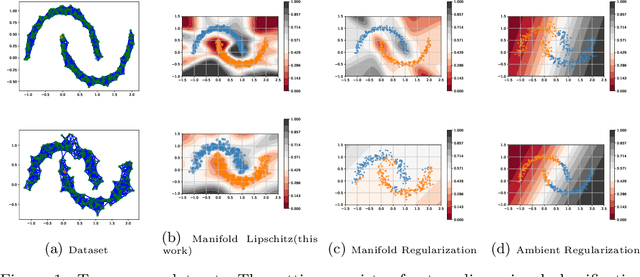
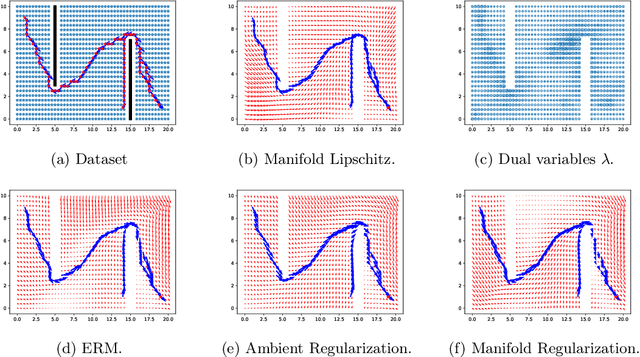
Smoothness and low dimensional structures play central roles in improving generalization and stability in learning and statistics. The combination of these properties has led to many advances in semi-supervised learning, generative modeling, and control of dynamical systems. However, learning smooth functions is generally challenging, except in simple cases such as learning linear or kernel models. Typical methods are either too conservative, relying on crude upper bounds such as spectral normalization, too lax, penalizing smoothness on average, or too computationally intensive, requiring the solution of large-scale semi-definite programs. These issues are only exacerbated when trying to simultaneously exploit low dimensionality using, e.g., manifolds. This work proposes to overcome these obstacles by combining techniques from semi-infinite constrained learning and manifold regularization. To do so, it shows that, under typical conditions, the problem of learning a Lipschitz continuous function on a manifold is equivalent to a dynamically weighted manifold regularization problem. This observation leads to a practical algorithm based on a weighted Laplacian penalty whose weights are adapted using stochastic gradient techniques. We prove that, under mild conditions, this method estimates the Lipschitz constant of the solution, learning a globally smooth solution as a byproduct. Numerical examples illustrate the advantages of using this method to impose global smoothness on manifolds as opposed to imposing smoothness on average.