On the Generalization Error of Meta Learning for the Gibbs Algorithm
Paper and Code
Apr 27, 2023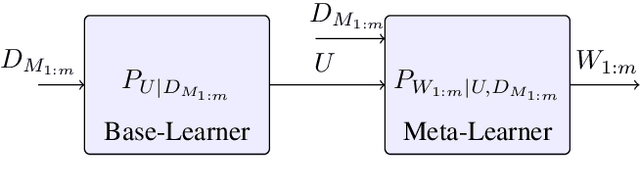
We analyze the generalization ability of joint-training meta learning algorithms via the Gibbs algorithm. Our exact characterization of the expected meta generalization error for the meta Gibbs algorithm is based on symmetrized KL information, which measures the dependence between all meta-training datasets and the output parameters, including task-specific and meta parameters. Additionally, we derive an exact characterization of the meta generalization error for the super-task Gibbs algorithm, in terms of conditional symmetrized KL information within the super-sample and super-task framework introduced in Steinke and Zakynthinou (2020) and Hellstrom and Durisi (2022) respectively. Our results also enable us to provide novel distribution-free generalization error upper bounds for these Gibbs algorithms applicable to meta learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge