An Information-theoretical Approach to Semi-supervised Learning under Covariate-shift
Paper and Code
Feb 24, 2022

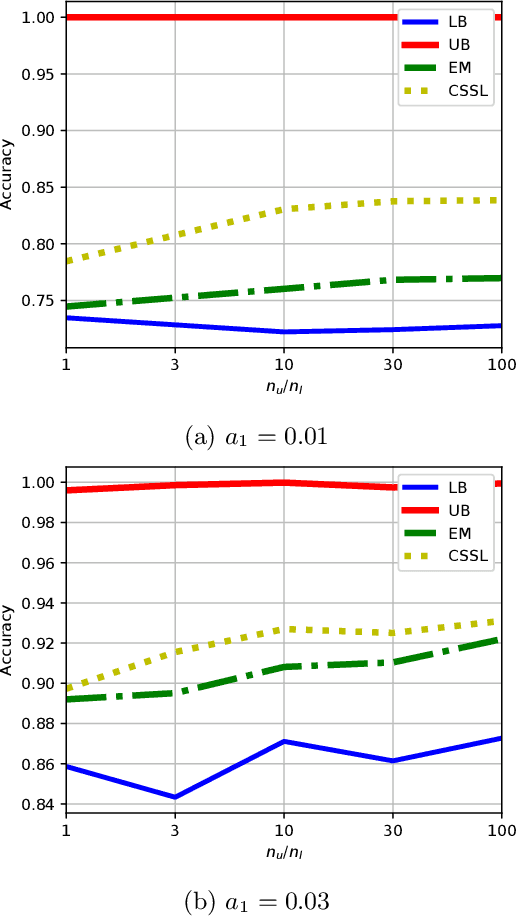
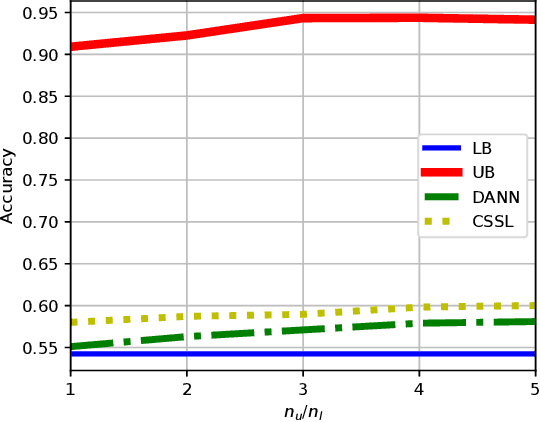
A common assumption in semi-supervised learning is that the labeled, unlabeled, and test data are drawn from the same distribution. However, this assumption is not satisfied in many applications. In many scenarios, the data is collected sequentially (e.g., healthcare) and the distribution of the data may change over time often exhibiting so-called covariate shifts. In this paper, we propose an approach for semi-supervised learning algorithms that is capable of addressing this issue. Our framework also recovers some popular methods, including entropy minimization and pseudo-labeling. We provide new information-theoretical based generalization error upper bounds inspired by our novel framework. Our bounds are applicable to both general semi-supervised learning and the covariate-shift scenario. Finally, we show numerically that our method outperforms previous approaches proposed for semi-supervised learning under the covariate shift.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge