Rewiring Networks for Graph Neural Network Training Using Discrete Geometry

Information over-squashing is a phenomenon of inefficient information propagation between distant nodes on networks. It is an important problem that is known to significantly impact the training of graph neural networks (GNNs), as the receptive field of a node grows exponentially. To mitigate this problem, a preprocessing procedure known as rewiring is often applied to the input network. In this paper, we investigate the use of discrete analogues of classical geometric notions of curvature to model information flow on networks and rewire them. We show that these classical notions achieve state-of-the-art performance in GNN training accuracy on a variety of real-world network datasets. Moreover, compared to the current state-of-the-art, these classical notions exhibit a clear advantage in computational runtime by several orders of magnitude.

Curved Markov Chain Monte Carlo for Network Learning

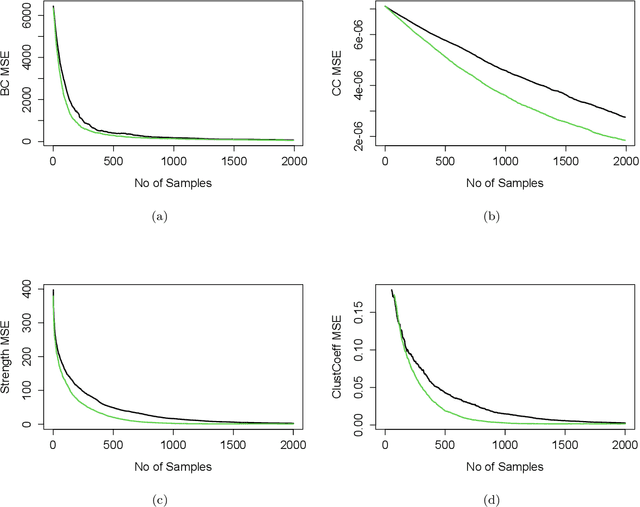
We present a geometrically enhanced Markov chain Monte Carlo sampler for networks based on a discrete curvature measure defined on graphs. Specifically, we incorporate the concept of graph Forman curvature into sampling procedures on both the nodes and edges of a network explicitly, via the transition probability of the Markov chain, as well as implicitly, via the target stationary distribution, which gives a novel, curved Markov chain Monte Carlo approach to learning networks. We show that integrating curvature into the sampler results in faster convergence to a wide range of network statistics demonstrated on deterministic networks drawn from real-world data.

Ricci Curvature Based Volumetric Segmentation of the Auditory Ossicles

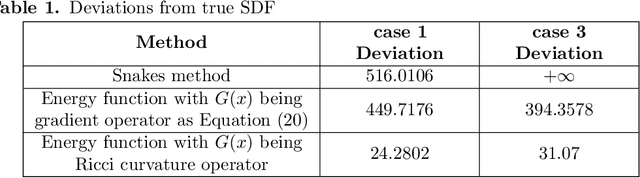
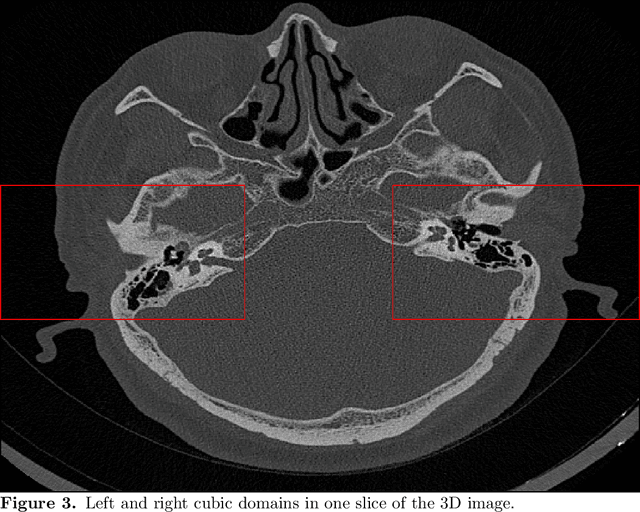
The auditory ossicles that are located in the middle ear are the smallest bones in the human body. Their damage will result in hearing loss. It is therefore important to be able to automatically diagnose ossicles' diseases based on Computed Tomography (CT) 3D imaging. However CT images usually include the whole head area, which is much larger than the bones of interest, thus the localization of the ossicles, followed by segmentation, both play a significant role in automatic diagnosis. The commonly employed local segmentation methods require manually selected initial points, which is a highly time consuming process. We therefore propose a completely automatic method to locate the ossicles which requires neither templates, nor manual labels. It relies solely on the connective properties of the auditory ossicles themselves, and their relationship with the surrounding tissue fluid. For the segmentation task, we define a novel energy function and obtain the shape of the ossicles from the 3D CT image by minimizing this new energy. Compared to the state-of-the-art methods which usually use the gradient operator and some normalization terms, we propose to add a Ricci curvature term to the commonly employed energy function. We compare our proposed method with the state-of-the-art methods and show that the performance of discrete Forman-Ricci curvature is superior to the others.

Isometric Embeddings in Imaging and Vision: Facts and Fiction

We explore the practicability of Nash's Embedding Theorem in vision and imaging sciences. In particular, we investigate the relevance of a result of Burago and Zalgaller regarding the existence of isometric embeddings of polyhedral surfaces in $\mathbb{R}^3$ and we show that their proof does not extended directly to higher dimensions.

Geometric approach to sampling and communication

Relationships that exist between the classical, Shannon-type, and geometric-based approaches to sampling are investigated. Some aspects of coding and communication through a Gaussian channel are considered. In particular, a constructive method to determine the quantizing dimension in Zador's theorem is provided. A geometric version of Shannon's Second Theorem is introduced. Applications to Pulse Code Modulation and Vector Quantization of Images are addressed.

Combinatorial Ricci Curvature and Laplacians for Image Processing

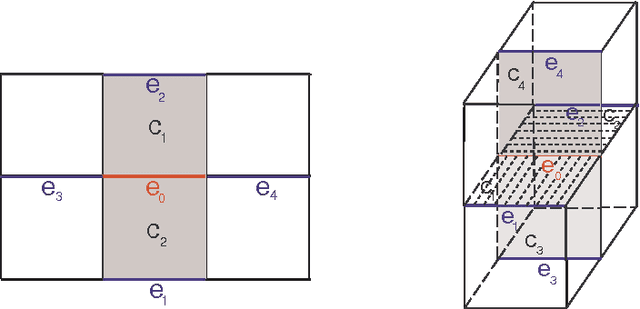
A new Combinatorial Ricci curvature and Laplacian operators for grayscale images are introduced and tested on 2D synthetic, natural and medical images. Analogue formulae for voxels are also obtained. These notions are based upon more general concepts developed by R. Forman. Further applications, in particular a fitting Ricci flow, are discussed.