A Survey of AI Methods for Geometry Preparation and Mesh Generation in Engineering Simulation

Artificial intelligence is beginning to ease long-standing bottlenecks in the CAD-to-mesh pipeline. This survey reviews recent advances where machine learning aids part classification, mesh quality prediction, and defeaturing. We explore methods that improve unstructured and block-structured meshing, support volumetric parameterizations, and accelerate parallel mesh generation. We also examine emerging tools for scripting automation, including reinforcement learning and large language models. Across these efforts, AI acts as an assistive technology, extending the capabilities of traditional geometry and meshing tools. The survey highlights representative methods, practical deployments, and key research challenges that will shape the next generation of data-driven meshing workflows.

OT-ALD: Aligning Latent Distributions with Optimal Transport for Accelerated Image-to-Image Translation

The Dual Diffusion Implicit Bridge (DDIB) is an emerging image-to-image (I2I) translation method that preserves cycle consistency while achieving strong flexibility. It links two independently trained diffusion models (DMs) in the source and target domains by first adding noise to a source image to obtain a latent code, then denoising it in the target domain to generate the translated image. However, this method faces two key challenges: (1) low translation efficiency, and (2) translation trajectory deviations caused by mismatched latent distributions. To address these issues, we propose a novel I2I translation framework, OT-ALD, grounded in optimal transport (OT) theory, which retains the strengths of DDIB-based approach. Specifically, we compute an OT map from the latent distribution of the source domain to that of the target domain, and use the mapped distribution as the starting point for the reverse diffusion process in the target domain. Our error analysis confirms that OT-ALD eliminates latent distribution mismatches. Moreover, OT-ALD effectively balances faster image translation with improved image quality. Experiments on four translation tasks across three high-resolution datasets show that OT-ALD improves sampling efficiency by 20.29% and reduces the FID score by 2.6 on average compared to the top-performing baseline models.

Robotic Manipulation via Imitation Learning: Taxonomy, Evolution, Benchmark, and Challenges

Robotic Manipulation (RM) is central to the advancement of autonomous robots, enabling them to interact with and manipulate objects in real-world environments. This survey focuses on RM methodologies that leverage imitation learning, a powerful technique that allows robots to learn complex manipulation skills by mimicking human demonstrations. We identify and analyze the most influential studies in this domain, selected based on community impact and intrinsic quality. For each paper, we provide a structured summary, covering the research purpose, technical implementation, hierarchical classification, input formats, key priors, strengths and limitations, and citation metrics. Additionally, we trace the chronological development of imitation learning techniques within RM policy (RMP), offering a timeline of key technological advancements. Where available, we report benchmark results and perform quantitative evaluations to compare existing methods. By synthesizing these insights, this review provides a comprehensive resource for researchers and practitioners, highlighting both the state of the art and the challenges that lie ahead in the field of robotic manipulation through imitation learning.

Point2Quad: Generating Quad Meshes from Point Clouds via Face Prediction

Quad meshes are essential in geometric modeling and computational mechanics. Although learning-based methods for triangle mesh demonstrate considerable advancements, quad mesh generation remains less explored due to the challenge of ensuring coplanarity, convexity, and quad-only meshes. In this paper, we present Point2Quad, the first learning-based method for quad-only mesh generation from point clouds. The key idea is learning to identify quad mesh with fused pointwise and facewise features. Specifically, Point2Quad begins with a k-NN-based candidate generation considering the coplanarity and squareness. Then, two encoders are followed to extract geometric and topological features that address the challenge of quad-related constraints, especially by combining in-depth quadrilaterals-specific characteristics. Subsequently, the extracted features are fused to train the classifier with a designed compound loss. The final results are derived after the refinement by a quad-specific post-processing. Extensive experiments on both clear and noise data demonstrate the effectiveness and superiority of Point2Quad, compared to baseline methods under comprehensive metrics.

Diff-CL: A Novel Cross Pseudo-Supervision Method for Semi-supervised Medical Image Segmentation

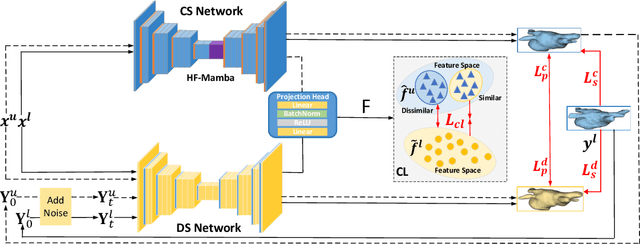
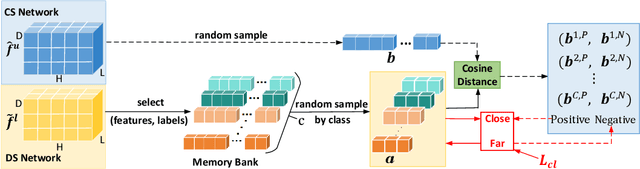
Semi-supervised learning utilizes insights from unlabeled data to improve model generalization, thereby reducing reliance on large labeled datasets. Most existing studies focus on limited samples and fail to capture the overall data distribution. We contend that combining distributional information with detailed information is crucial for achieving more robust and accurate segmentation results. On the one hand, with its robust generative capabilities, diffusion models (DM) learn data distribution effectively. However, it struggles with fine detail capture, leading to generated images with misleading details. Combining DM with convolutional neural networks (CNNs) enables the former to learn data distribution while the latter corrects fine details. While capturing complete high-frequency details by CNNs requires substantial computational resources and is susceptible to local noise. On the other hand, given that both labeled and unlabeled data come from the same distribution, we believe that regions in unlabeled data similar to overall class semantics to labeled data are likely to belong to the same class, while regions with minimal similarity are less likely to. This work introduces a semi-supervised medical image segmentation framework from the distribution perspective (Diff-CL). Firstly, we propose a cross-pseudo-supervision learning mechanism between diffusion and convolution segmentation networks. Secondly, we design a high-frequency mamba module to capture boundary and detail information globally. Finally, we apply contrastive learning for label propagation from labeled to unlabeled data. Our method achieves state-of-the-art (SOTA) performance across three datasets, including left atrium, brain tumor, and NIH pancreas datasets.

Solving Prior Distribution Mismatch in Diffusion Models via Optimal Transport

In recent years, the knowledge surrounding diffusion models(DMs) has grown significantly, though several theoretical gaps remain. Particularly noteworthy is prior error, defined as the discrepancy between the termination distribution of the forward process and the initial distribution of the reverse process. To address these deficiencies, this paper explores the deeper relationship between optimal transport(OT) theory and DMs with discrete initial distribution. Specifically, we demonstrate that the two stages of DMs fundamentally involve computing time-dependent OT. However, unavoidable prior error result in deviation during the reverse process under quadratic transport cost. By proving that as the diffusion termination time increases, the probability flow exponentially converges to the gradient of the solution to the classical Monge-Amp\`ere equation, we establish a vital link between these fields. Therefore, static OT emerges as the most intrinsic single-step method for bridging this theoretical potential gap. Additionally, we apply these insights to accelerate sampling in both unconditional and conditional generation scenarios. Experimental results across multiple image datasets validate the effectiveness of our approach.

HOTS3D: Hyper-Spherical Optimal Transport for Semantic Alignment of Text-to-3D Generation

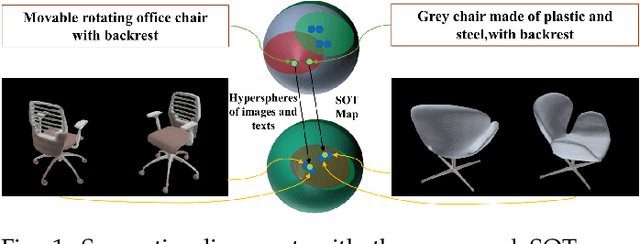
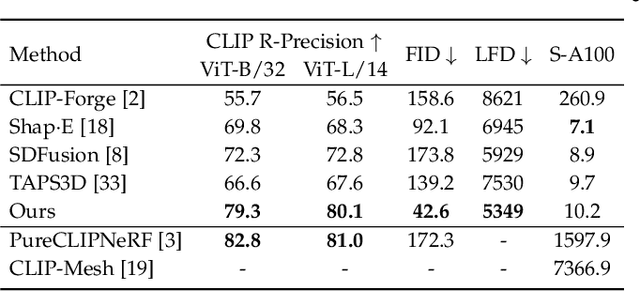
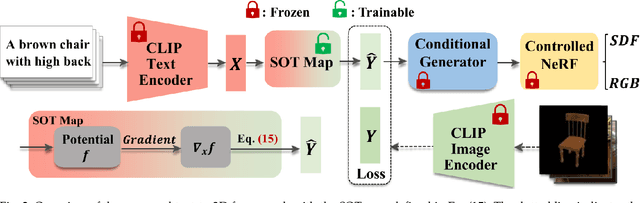
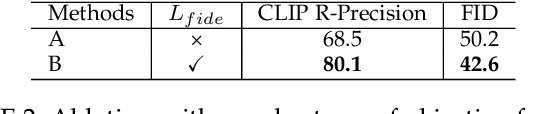
Recent CLIP-guided 3D generation methods have achieved promising results but struggle with generating faithful 3D shapes that conform with input text due to the gap between text and image embeddings. To this end, this paper proposes HOTS3D which makes the first attempt to effectively bridge this gap by aligning text features to the image features with spherical optimal transport (SOT). However, in high-dimensional situations, solving the SOT remains a challenge. To obtain the SOT map for high-dimensional features obtained from CLIP encoding of two modalities, we mathematically formulate and derive the solution based on Villani's theorem, which can directly align two hyper-sphere distributions without manifold exponential maps. Furthermore, we implement it by leveraging input convex neural networks (ICNNs) for the optimal Kantorovich potential. With the optimally mapped features, a diffusion-based generator and a Nerf-based decoder are subsequently utilized to transform them into 3D shapes. Extensive qualitative and qualitative comparisons with state-of-the-arts demonstrate the superiority of the proposed HOTS3D for 3D shape generation, especially on the consistency with text semantics.

MergeNet: Explicit Mesh Reconstruction from Sparse Point Clouds via Edge Prediction

This paper introduces a novel method for reconstructing meshes from sparse point clouds by predicting edge connection. Existing implicit methods usually produce superior smooth and watertight meshes due to the isosurface extraction algorithms~(e.g., Marching Cubes). However, these methods become memory and computationally intensive with increasing resolution. Explicit methods are more efficient by directly forming the face from points. Nevertheless, the challenge of selecting appropriate faces from enormous candidates often leads to undesirable faces and holes. Moreover, the reconstruction performance of both approaches tends to degrade when the point cloud gets sparse. To this end, we propose MEsh Reconstruction via edGE~(MergeNet), which converts mesh reconstruction into local connectivity prediction problems. Specifically, MergeNet learns to extract the features of candidate edges and regress their distances to the underlying surface. Consequently, the predicted distance is utilized to filter out edges that lay on surfaces. Finally, the meshes are reconstructed by refining the triangulations formed by these edges. Extensive experiments on synthetic and real-scanned datasets demonstrate the superiority of MergeNet to SoTA explicit methods.

Learning Unsigned Distance Fields from Local Shape Functions for 3D Surface Reconstruction

Unsigned distance fields (UDFs) provide a versatile framework for representing a diverse array of 3D shapes, encompassing both watertight and non-watertight geometries. Traditional UDF learning methods typically require extensive training on large datasets of 3D shapes, which is costly and often necessitates hyperparameter adjustments for new datasets. This paper presents a novel neural framework, LoSF-UDF, for reconstructing surfaces from 3D point clouds by leveraging local shape functions to learn UDFs. We observe that 3D shapes manifest simple patterns within localized areas, prompting us to create a training dataset of point cloud patches characterized by mathematical functions that represent a continuum from smooth surfaces to sharp edges and corners. Our approach learns features within a specific radius around each query point and utilizes an attention mechanism to focus on the crucial features for UDF estimation. This method enables efficient and robust surface reconstruction from point clouds without the need for shape-specific training. Additionally, our method exhibits enhanced resilience to noise and outliers in point clouds compared to existing methods. We present comprehensive experiments and comparisons across various datasets, including synthetic and real-scanned point clouds, to validate our method's efficacy.

Global Parameterization-based Texture Space Optimization

Texture mapping is a common technology in the area of computer graphics, it maps the 3D surface space onto the 2D texture space. However, the loose texture space will reduce the efficiency of data storage and GPU memory addressing in the rendering process. Many of the existing methods focus on repacking given textures, but they still suffer from high computational cost and hardly produce a wholly tight texture space. In this paper, we propose a method to optimize the texture space and produce a new texture mapping which is compact based on global parameterization. The proposed method is computationally robust and efficient. Experiments show the effectiveness of the proposed method and the potency in improving the storage and rendering efficiency.