Learning Unsigned Distance Fields from Local Shape Functions for 3D Surface Reconstruction

Unsigned distance fields (UDFs) provide a versatile framework for representing a diverse array of 3D shapes, encompassing both watertight and non-watertight geometries. Traditional UDF learning methods typically require extensive training on large datasets of 3D shapes, which is costly and often necessitates hyperparameter adjustments for new datasets. This paper presents a novel neural framework, LoSF-UDF, for reconstructing surfaces from 3D point clouds by leveraging local shape functions to learn UDFs. We observe that 3D shapes manifest simple patterns within localized areas, prompting us to create a training dataset of point cloud patches characterized by mathematical functions that represent a continuum from smooth surfaces to sharp edges and corners. Our approach learns features within a specific radius around each query point and utilizes an attention mechanism to focus on the crucial features for UDF estimation. This method enables efficient and robust surface reconstruction from point clouds without the need for shape-specific training. Additionally, our method exhibits enhanced resilience to noise and outliers in point clouds compared to existing methods. We present comprehensive experiments and comparisons across various datasets, including synthetic and real-scanned point clouds, to validate our method's efficacy.

Topology-Aware Latent Diffusion for 3D Shape Generation

We introduce a new generative model that combines latent diffusion with persistent homology to create 3D shapes with high diversity, with a special emphasis on their topological characteristics. Our method involves representing 3D shapes as implicit fields, then employing persistent homology to extract topological features, including Betti numbers and persistence diagrams. The shape generation process consists of two steps. Initially, we employ a transformer-based autoencoding module to embed the implicit representation of each 3D shape into a set of latent vectors. Subsequently, we navigate through the learned latent space via a diffusion model. By strategically incorporating topological features into the diffusion process, our generative module is able to produce a richer variety of 3D shapes with different topological structures. Furthermore, our framework is flexible, supporting generation tasks constrained by a variety of inputs, including sparse and partial point clouds, as well as sketches. By modifying the persistence diagrams, we can alter the topology of the shapes generated from these input modalities.

Non-rigid 3D shape retrieval based on multi-view metric learning

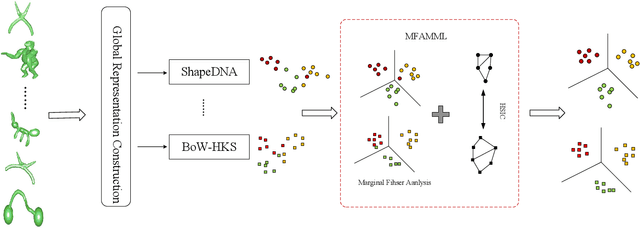
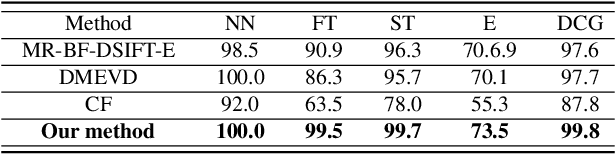
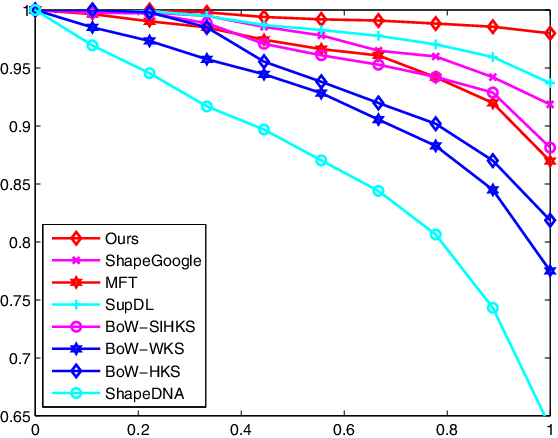
This study presents a novel multi-view metric learning algorithm, which aims to improve 3D non-rigid shape retrieval. With the development of non-rigid 3D shape analysis, there exist many shape descriptors. The intrinsic descriptors can be explored to construct various intrinsic representations for non-rigid 3D shape retrieval task. The different intrinsic representations (features) focus on different geometric properties to describe the same 3D shape, which makes the representations are related. Therefore, it is possible and necessary to learn multiple metrics for different representations jointly. We propose an effective multi-view metric learning algorithm by extending the Marginal Fisher Analysis (MFA) into the multi-view domain, and exploring Hilbert-Schmidt Independence Criteria (HSCI) as a diversity term to jointly learning the new metrics. The different classes can be separated by MFA in our method. Meanwhile, HSCI is exploited to make the multiple representations to be consensus. The learned metrics can reduce the redundancy between the multiple representations, and improve the accuracy of the retrieval results. Experiments are performed on SHREC'10 benchmarks, and the results show that the proposed method outperforms the state-of-the-art non-rigid 3D shape retrieval methods.