PTL-Diffusion: Manifold-Aware Diffusion with Periodic Terminal Laws

Standard diffusion models typically use a single time-homogeneous Gaussian terminal distribution as the reference law for generation. While this choice is analytically convenient and empirically powerful, it provides little explicit structure for data concentrated near low-dimensional manifolds, where different regions of the data distribution may correspond to distinct local geometric or semantic factors. As a result, the reverse model must recover manifold-level structure almost entirely from an unstructured terminal reference distribution. We propose PTL-Diffusion, a proof-of-concept diffusion framework whose forward noising process converges to a nonconstant periodic family of Gaussian terminal laws rather than to a single invariant law. Unlike a phase-conditioned DDPM, where phase information only enters the denoising network while the forward process remains unchanged, PTL-Diffusion embeds phase structure directly into the forward noising dynamics. The proposed construction remains close to standard denoising diffusion models: for a periodically forced Ornstein--Uhlenbeck-type forward process, we derive closed-form forward marginals, the limiting periodic Gaussian terminal family, and explicit Gaussian reverse posteriors, enabling standard noise-prediction training. We also introduce an invariant-average regularization term coupling the phase-conditioned reverse dynamics through the averaged periodic reference law. Experiments on torus and cylinder point-cloud benchmarks and the Olivetti face dataset show that PTL-Diffusion improves manifold-level distributional matching over matched DDPM baselines, reducing phase-conditioned errors, feature-space covariance errors, and nearest-neighbour manifold distances. These results suggest structured terminal reference laws as a promising direction, while motivating more expressive phase constructions and larger-scale evaluations.

Superpixel-Based Image Segmentation Using Squared 2-Wasserstein Distances

We present an efficient method for image segmentation in the presence of strong inhomogeneities. The approach can be interpreted as a two-level clustering procedure: pixels are first grouped into superpixels via a linear least-squares assignment problem, which can be viewed as a special case of a discrete optimal transport (OT) problem, and these superpixels are subsequently greedily merged into object-level segments using the squared 2-Wasserstein distance between their empirical distributions. In contrast to conventional superpixel merging strategies based on mean-color distances, our framework employs a distributional OT distance, yielding a mathematically unified formulation across both clustering levels. Numerical experiments demonstrate that this perspective leads to improved segmentation accuracy on challenging images while retaining high computational efficiency.

Ricci Curvature Based Volumetric Segmentation of the Auditory Ossicles

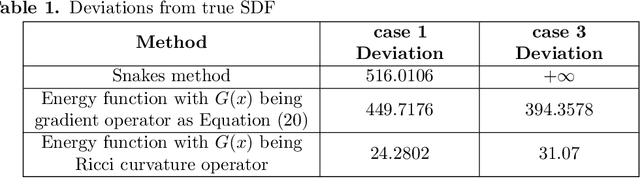
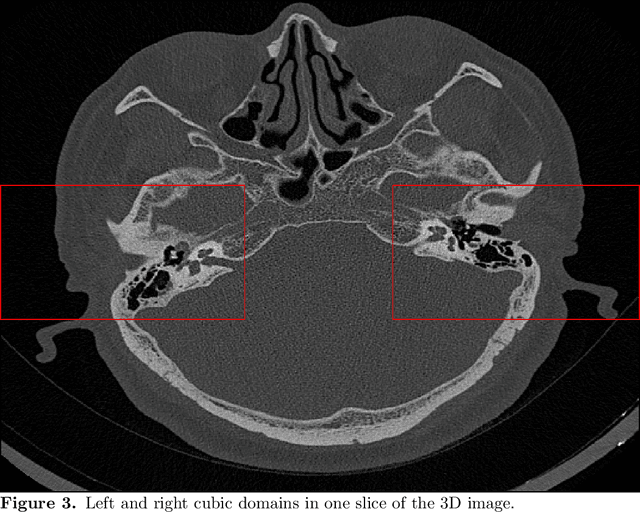
The auditory ossicles that are located in the middle ear are the smallest bones in the human body. Their damage will result in hearing loss. It is therefore important to be able to automatically diagnose ossicles' diseases based on Computed Tomography (CT) 3D imaging. However CT images usually include the whole head area, which is much larger than the bones of interest, thus the localization of the ossicles, followed by segmentation, both play a significant role in automatic diagnosis. The commonly employed local segmentation methods require manually selected initial points, which is a highly time consuming process. We therefore propose a completely automatic method to locate the ossicles which requires neither templates, nor manual labels. It relies solely on the connective properties of the auditory ossicles themselves, and their relationship with the surrounding tissue fluid. For the segmentation task, we define a novel energy function and obtain the shape of the ossicles from the 3D CT image by minimizing this new energy. Compared to the state-of-the-art methods which usually use the gradient operator and some normalization terms, we propose to add a Ricci curvature term to the commonly employed energy function. We compare our proposed method with the state-of-the-art methods and show that the performance of discrete Forman-Ricci curvature is superior to the others.