Curved Markov Chain Monte Carlo for Network Learning
Paper and Code
Oct 11, 2021


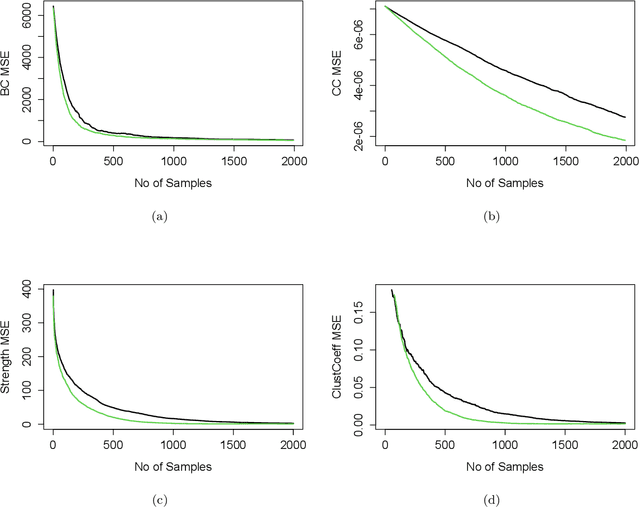
We present a geometrically enhanced Markov chain Monte Carlo sampler for networks based on a discrete curvature measure defined on graphs. Specifically, we incorporate the concept of graph Forman curvature into sampling procedures on both the nodes and edges of a network explicitly, via the transition probability of the Markov chain, as well as implicitly, via the target stationary distribution, which gives a novel, curved Markov chain Monte Carlo approach to learning networks. We show that integrating curvature into the sampler results in faster convergence to a wide range of network statistics demonstrated on deterministic networks drawn from real-world data.
* 12 pages, 5 figures. To appear in Studies in Computational
Intelligence: Proceedings of The 10th International Conference on Complex
Networks and Their Applications (2021)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge