Distortion measure of spectrograms for classification of respiratory diseases

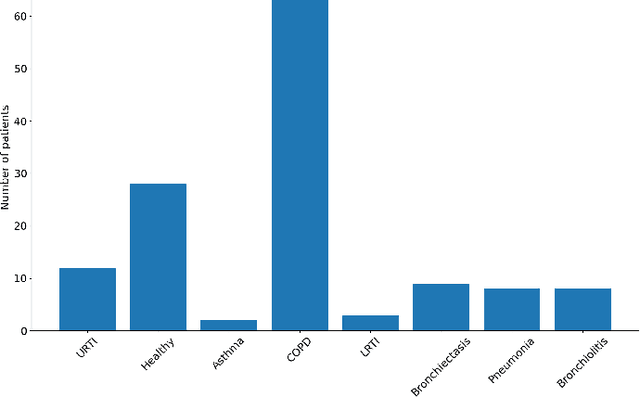
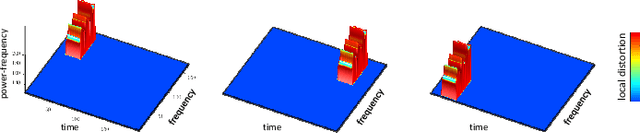
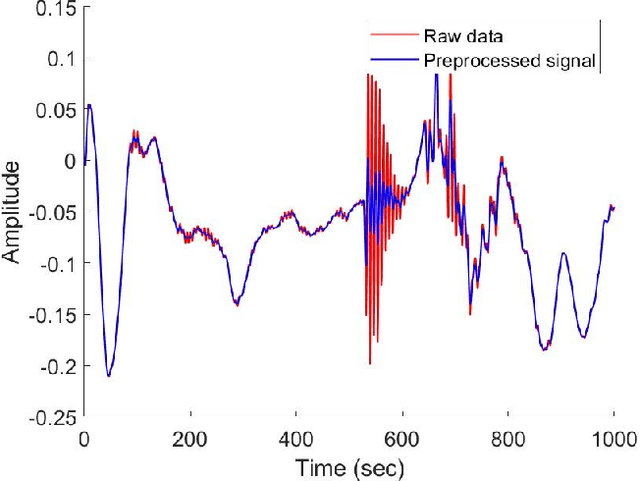
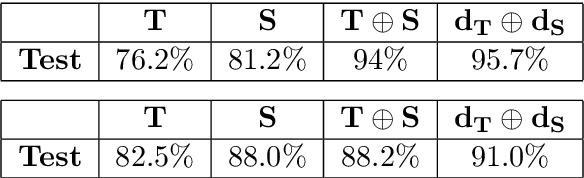
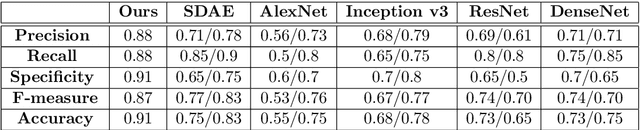
A new method for the classification of respiratory diseases is presented. The method is based on a novel class of features, extracted from pulmonary sounds, by parameterizing their spectrograms that are represented as surfaces, and by utilizing geometrical distortions defined with reference to these surfaces. This method yields a set of highly descriptive features for the analysis of pulmonary sound recordings. Furthermore, by combining these features with Mel-frequency cepstral coefficients, we introduce a powerful model for the automatic diagnosis of common respiratory pathologies. Compared with baseline methods, our model achieves superior results for binary and multi-class classifications of common respiratory diseases. Our new approach to the classification of one-dimensional signals is applicable to other signals in the context of their representations in combined spaces or manifolds.

Texture and Structure Two-view Classification of Images

Textural and structural features can be regraded as "two-view" feature sets. Inspired by the recent progress in multi-view learning, we propose a novel two-view classification method that models each feature set and optimizes the process of merging these views efficiently. Examples of implementation of this approach in classification of real-world data are presented, with special emphasis on medical images. We firstly decompose fully-textured images into two layers of representation, corresponding to natural stochastic textures (NST) and structural layer, respectively. The structural, edge-and-curve-type, information is mostly represented by the local spatial phase, whereas, the pure NST has random phase and is characterized by Gaussianity and self-similarity. Therefore, the NST is modeled by the 2D self-similar process, fractional Brownian motion (fBm). The Hurst parameter, characteristic of fBm, specifies the roughness or irregularity of the texture. This leads us to its estimation and implementation along other features extracted from the structure layer, to build the "two-view" features sets used in our classification scheme. A shallow neural net (NN) is exploited to execute the process of merging these feature sets, in a straightforward and efficient manner.

On the Self-Similarity of Natural Stochastic Textures

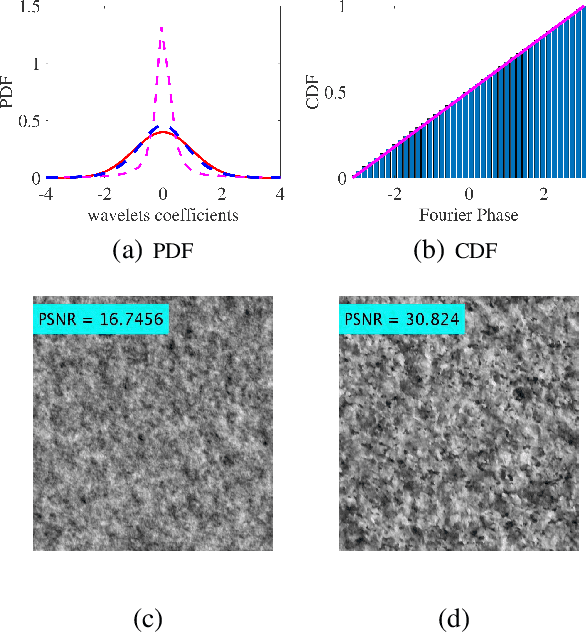
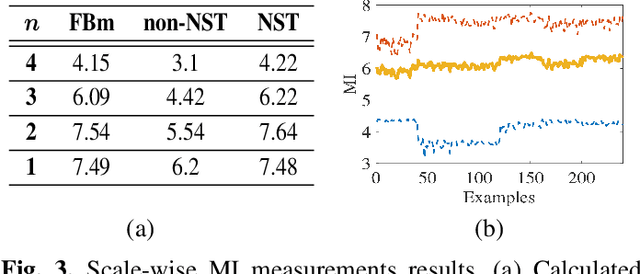
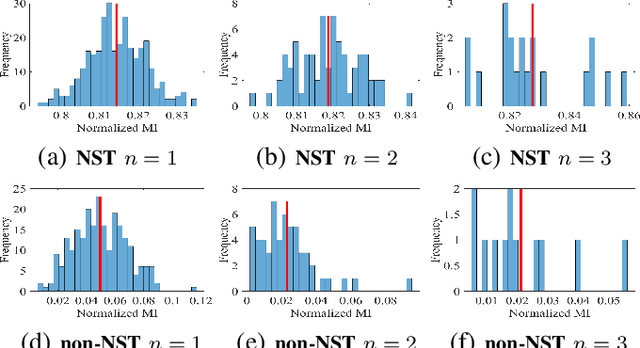
Self-similarity is the essence of fractal images and, as such, characterizes natural stochastic textures. This paper is concerned with the property of self-similarity in the statistical sense in the case of fully-textured images that contain both stochastic texture and structural (mostly deterministic) information. We firstly decompose a textured image into two layers corresponding to its texture and structure, and show that the layer representing the stochastic texture is characterized by random phase of uniform distribution, unlike the phase of the structured information which is coherent. The uniform distribution of the the random phase is verified by using a suitable hypothesis testing framework. We proceed by proposing two approaches to assessment of self-similarity. The first is based on patch-wise calculation of the mutual information, while the second measures the mutual information that exists across scales. Quantifying the extent of self-similarity by means of mutual information is of paramount importance in the analysis of natural stochastic textures that are encountered in medical imaging, geology, agriculture and in computer vision algorithms that are designed for application on fully-textures images.

Modelling local phase of images and textures with applications in phase denoising and phase retrieval

The Fourier magnitude has been studied extensively, but less effort has been devoted to the Fourier phase, despite its well-established importance in image representation. Global phase was shown to be more important for image representation than the magnitude, whereas local phase, exhibited in Gabor filters, has been used for analysis purposes in detecting image contours and edges. Neither global nor local phase has been modelled in closed form, suitable for Bayesian estimation. In this work, we analyze the local phase of textured images and propose a local (Markovian) model for local phase coefficients. This model is Gaussian-mixture-based, learned from the graph representation of images, based on their complex wavelet decomposition. We demonstrate the applicability of the model in restoration of images with noisy local phase and in image retrieval, where we show superior performance to the well-known hybrid input-output (HIO) method. We also provide a framework for application of the model in a general setup of image processing.

Geometric approach to sampling and communication

Relationships that exist between the classical, Shannon-type, and geometric-based approaches to sampling are investigated. Some aspects of coding and communication through a Gaussian channel are considered. In particular, a constructive method to determine the quantizing dimension in Zador's theorem is provided. A geometric version of Shannon's Second Theorem is introduced. Applications to Pulse Code Modulation and Vector Quantization of Images are addressed.

Combinatorial Ricci Curvature and Laplacians for Image Processing

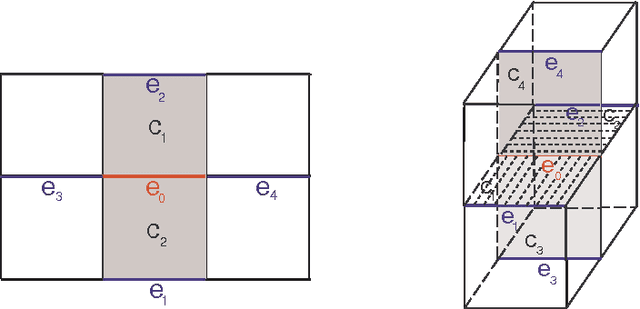
A new Combinatorial Ricci curvature and Laplacian operators for grayscale images are introduced and tested on 2D synthetic, natural and medical images. Analogue formulae for voxels are also obtained. These notions are based upon more general concepts developed by R. Forman. Further applications, in particular a fitting Ricci flow, are discussed.