Learning Linear Non-Gaussian Polytree Models
Paper and Code
Aug 13, 2022

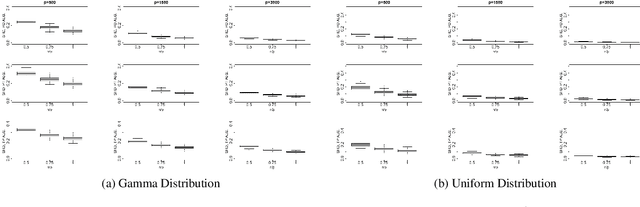
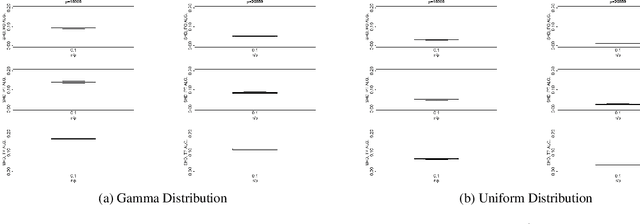
In the context of graphical causal discovery, we adapt the versatile framework of linear non-Gaussian acyclic models (LiNGAMs) to propose new algorithms to efficiently learn graphs that are polytrees. Our approach combines the Chow--Liu algorithm, which first learns the undirected tree structure, with novel schemes to orient the edges. The orientation schemes assess algebraic relations among moments of the data-generating distribution and are computationally inexpensive. We establish high-dimensional consistency results for our approach and compare different algorithmic versions in numerical experiments.
View paper on
 OpenReview
OpenReview
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge