Over-squashing in Spatiotemporal Graph Neural Networks

Graph Neural Networks (GNNs) have achieved remarkable success across various domains. However, recent theoretical advances have identified fundamental limitations in their information propagation capabilities, such as over-squashing, where distant nodes fail to effectively exchange information. While extensively studied in static contexts, this issue remains unexplored in Spatiotemporal GNNs (STGNNs), which process sequences associated with graph nodes. Nonetheless, the temporal dimension amplifies this challenge by increasing the information that must be propagated. In this work, we formalize the spatiotemporal over-squashing problem and demonstrate its distinct characteristics compared to the static case. Our analysis reveals that counterintuitively, convolutional STGNNs favor information propagation from points temporally distant rather than close in time. Moreover, we prove that architectures that follow either time-and-space or time-then-space processing paradigms are equally affected by this phenomenon, providing theoretical justification for computationally efficient implementations. We validate our findings on synthetic and real-world datasets, providing deeper insights into their operational dynamics and principled guidance for more effective designs.

On Measuring Long-Range Interactions in Graph Neural Networks

Long-range graph tasks -- those dependent on interactions between distant nodes -- are an open problem in graph neural network research. Real-world benchmark tasks, especially the Long Range Graph Benchmark, have become popular for validating the long-range capability of proposed architectures. However, this is an empirical approach that lacks both robustness and theoretical underpinning; a more principled characterization of the long-range problem is required. To bridge this gap, we formalize long-range interactions in graph tasks, introduce a range measure for operators on graphs, and validate it with synthetic experiments. We then leverage our measure to examine commonly used tasks and architectures, and discuss to what extent they are, in fact, long-range. We believe our work advances efforts to define and address the long-range problem on graphs, and that our range measure will aid evaluation of new datasets and architectures.

Bundle Neural Networks for message diffusion on graphs

The dominant paradigm for learning on graph-structured data is message passing. Despite being a strong inductive bias, the local message passing mechanism suffers from pathological issues such as over-smoothing, over-squashing, and limited node-level expressivity. To address these limitations we propose Bundle Neural Networks (BuNN), a new type of GNN that operates via message diffusion over flat vector bundles - structures analogous to connections on Riemannian manifolds that augment the graph by assigning to each node a vector space and an orthogonal map. A BuNN layer evolves the features according to a diffusion-type partial differential equation. When discretized, BuNNs are a special case of Sheaf Neural Networks (SNNs), a recently proposed MPNN capable of mitigating over-smoothing. The continuous nature of message diffusion enables BuNNs to operate on larger scales of the graph and, therefore, to mitigate over-squashing. Finally, we prove that BuNN can approximate any feature transformation over nodes on any (potentially infinite) family of graphs given injective positional encodings, resulting in universal node-level expressivity. We support our theory via synthetic experiments and showcase the strong empirical performance of BuNNs over a range of real-world tasks, achieving state-of-the-art results on several standard benchmarks in transductive and inductive settings.

A Topological characterisation of Weisfeiler-Leman equivalence classes

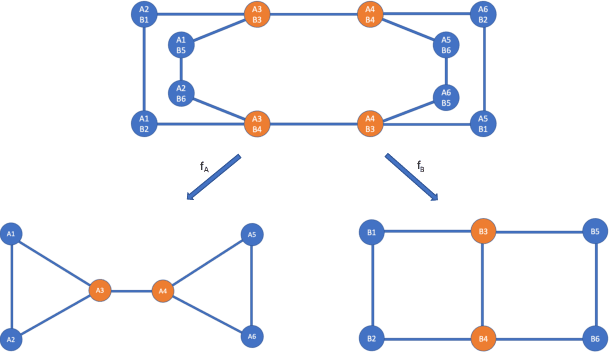
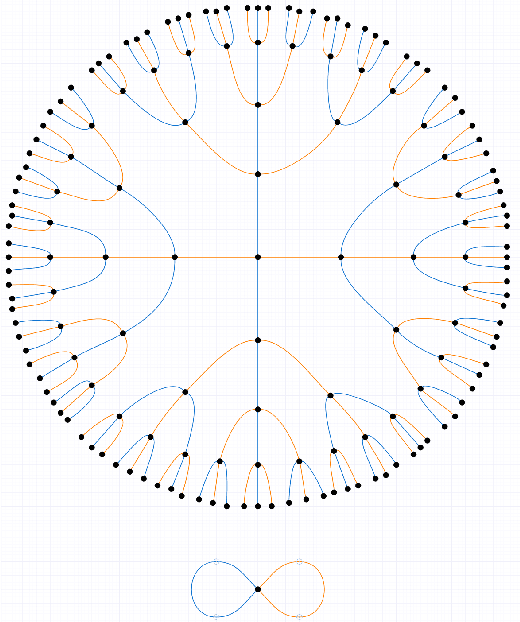
Graph Neural Networks (GNNs) are learning models aimed at processing graphs and signals on graphs. The most popular and successful GNNs are based on message passing schemes. Such schemes inherently have limited expressive power when it comes to distinguishing two non-isomorphic graphs. In this article, we rely on the theory of covering spaces to fully characterize the classes of graphs that GNNs cannot distinguish. We then generate arbitrarily many non-isomorphic graphs that cannot be distinguished by GNNs, leading to the GraphCovers dataset. We also show that the number of indistinguishable graphs in our dataset grows super-exponentially with the number of nodes. Finally, we test the GraphCovers dataset on several GNN architectures, showing that none of them can distinguish any two graphs it contains.