A Topological characterisation of Weisfeiler-Leman equivalence classes
Paper and Code
Jun 23, 2022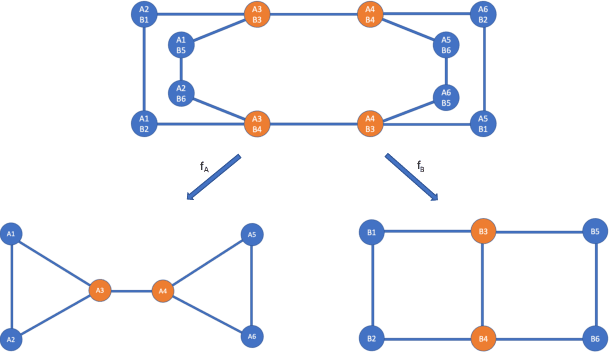

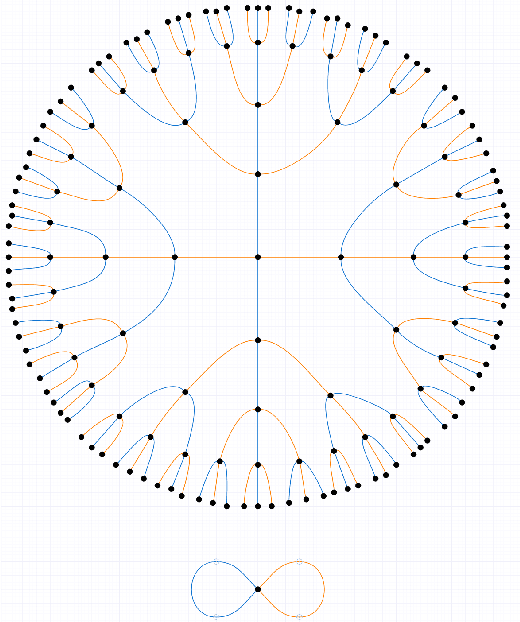
Graph Neural Networks (GNNs) are learning models aimed at processing graphs and signals on graphs. The most popular and successful GNNs are based on message passing schemes. Such schemes inherently have limited expressive power when it comes to distinguishing two non-isomorphic graphs. In this article, we rely on the theory of covering spaces to fully characterize the classes of graphs that GNNs cannot distinguish. We then generate arbitrarily many non-isomorphic graphs that cannot be distinguished by GNNs, leading to the GraphCovers dataset. We also show that the number of indistinguishable graphs in our dataset grows super-exponentially with the number of nodes. Finally, we test the GraphCovers dataset on several GNN architectures, showing that none of them can distinguish any two graphs it contains.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge