Whole-Body Model-Predictive Control of Legged Robots with MuJoCo

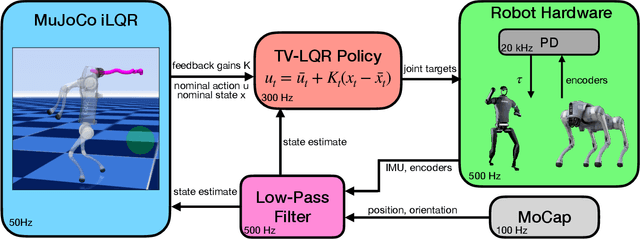
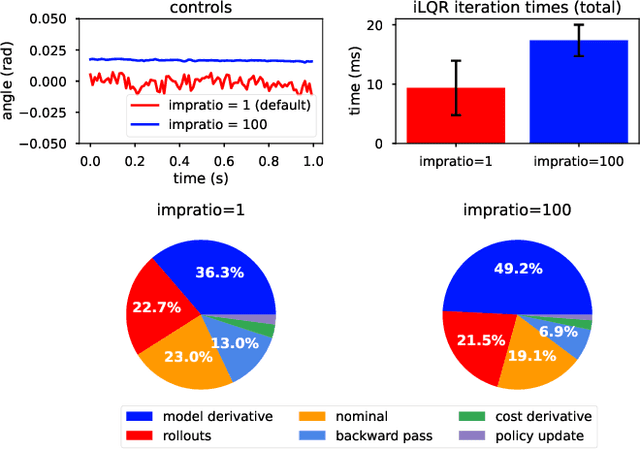
We demonstrate the surprising real-world effectiveness of a very simple approach to whole-body model-predictive control (MPC) of quadruped and humanoid robots: the iterative LQR (iLQR) algorithm with MuJoCo dynamics and finite-difference approximated derivatives. Building upon the previous success of model-based behavior synthesis and control of locomotion and manipulation tasks with MuJoCo in simulation, we show that these policies can easily generalize to the real world with few sim-to-real considerations. Our baseline method achieves real-time whole-body MPC on a variety of hardware experiments, including dynamic quadruped locomotion, quadruped walking on two legs, and full-sized humanoid bipedal locomotion. We hope this easy-to-reproduce hardware baseline lowers the barrier to entry for real-world whole-body MPC research and contributes to accelerating research velocity in the community. Our code and experiment videos will be available online at:https://johnzhang3.github.io/mujoco_ilqr

Differentiable Physics Simulation of Dynamics-Augmented Neural Objects

We present a differentiable pipeline for simulating the motion of objects that represent their geometry as a continuous density field parameterized as a deep network. This includes Neural Radiance Fields (NeRFs), and other related models. From the density field, we estimate the dynamical properties of the object, including its mass, center of mass, and inertia matrix. We then introduce a differentiable contact model based on the density field for computing normal and friction forces resulting from collisions. This allows a robot to autonomously build object models that are visually and dynamically accurate from still images and videos of objects in motion. The resulting Dynamics-Augmented Neural Objects (DANOs) are simulated with an existing differentiable simulation engine, Dojo, interacting with other standard simulation objects, such as spheres, planes, and robots specified as URDFs. A robot can use this simulation to optimize grasps and manipulation trajectories of neural objects, or to improve the neural object models through gradient-based real-to-simulation transfer. We demonstrate the pipeline to learn the coefficient of friction of a bar of soap from a real video of the soap sliding on a table. We also learn the coefficient of friction and mass of a Stanford bunny through interactions with a Panda robot arm from synthetic data, and we optimize trajectories in simulation for the Panda arm to push the bunny to a goal location.

Differentiable Collision Detection for a Set of Convex Primitives

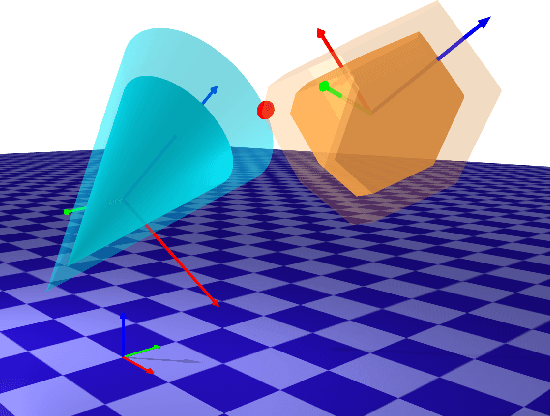
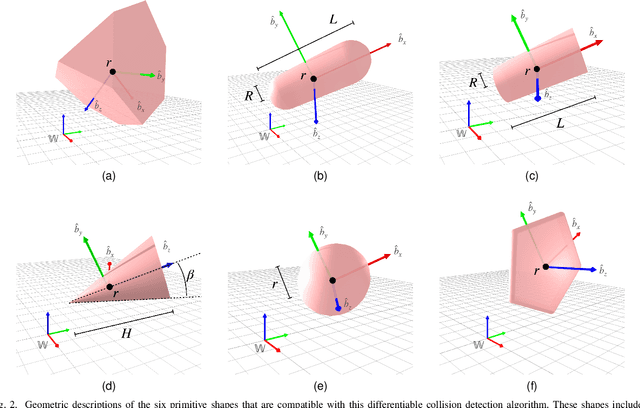
Collision detection between objects is critical for simulation, control, and learning for robotic systems. However, existing collision detection routines are inherently non-differentiable, limiting their usefulness in optimization-based algorithms. In this work, we propose a fully differentiable collision-detection framework that reasons about distances between a set of composable and highly expressive convex primitive shapes. This is achieved by formulating the collision detection problem as a convex optimization problem that seeks to find the minimum uniform scaling to be applied to each object before there is an intersection. The optimization problem is fully differentiable and is able to return both the collision detection status as well as the contact points on each object.

DiffPills: Differentiable Collision Detection for Capsules and Padded Polygons

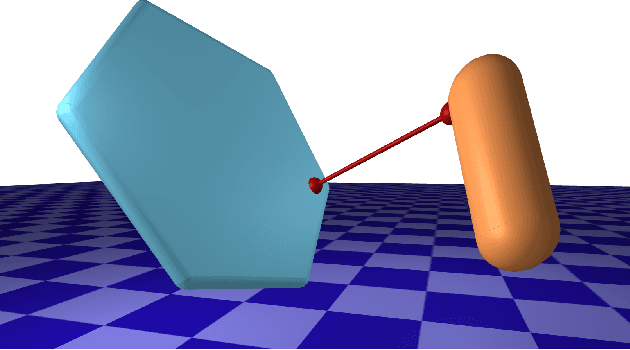
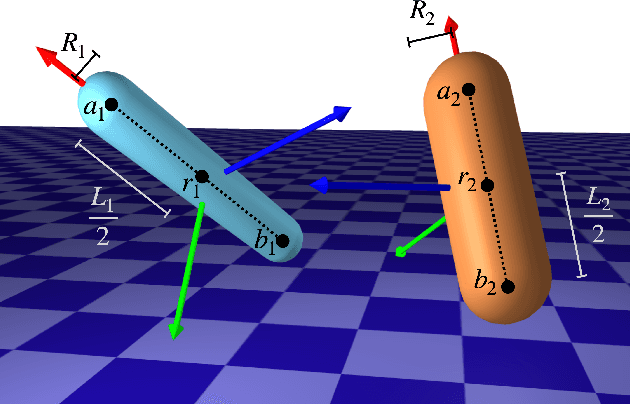
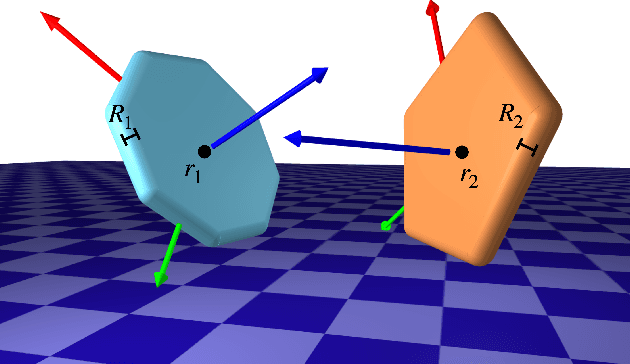
Collision detection plays an important role in simulation, control, and learning for robotic systems. However, no existing method is differentiable with respect to the configurations of the objects, greatly limiting the sort of algorithms that can be built on top of collision detection. In this work, we propose a set of differentiable collision detection algorithms between capsules and padded polygons by formulating these problems as differentiable convex quadratic programs. The resulting algorithms are able to return a proximity value indicating if a collision has taken place, as well as the closest points between objects, all of which are differentiable. As a result, they can be used reliably within other gradient-based optimization methods, including trajectory optimization, state estimation, and reinforcement learning methods.

CALIPSO: A Differentiable Solver for Trajectory Optimization with Conic and Complementarity Constraints

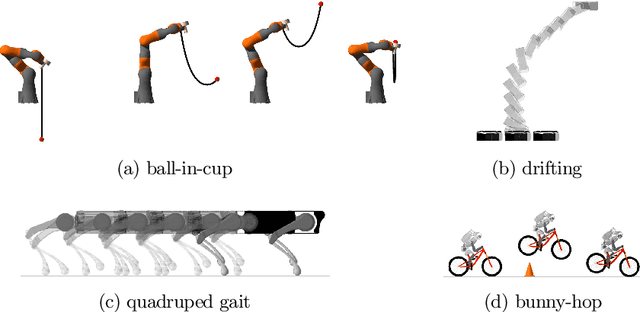
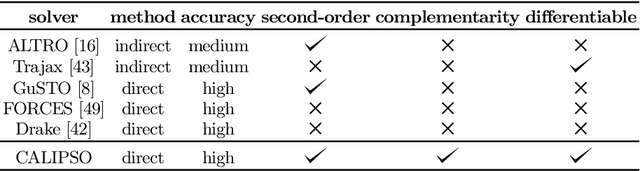
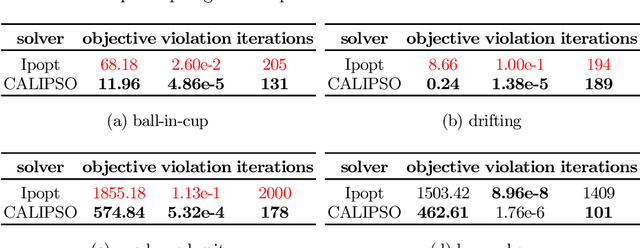
We present a new solver for non-convex trajectory optimization problems that is specialized for robotics applications. CALIPSO, or the Conic Augmented Lagrangian Interior-Point SOlver, combines several strategies for constrained numerical optimization to natively handle second-order cones and complementarity constraints. It reliably solves challenging motion-planning problems that include contact-implicit formulations of impacts and Coulomb friction, thrust limits subject to conic constraints, and state-triggered constraints where general-purpose nonlinear programming solvers like SNOPT and Ipopt fail to converge. Additionally, CALIPSO supports efficient differentiation of solutions with respect to problem data, enabling bi-level optimization applications like auto-tuning of feedback policies. Reliable convergence of the solver is demonstrated on a range of problems from manipulation, locomotion, and aerospace domains. An open-source implementation of this solver is available.

Dojo: A Differentiable Simulator for Robotics

We present a differentiable rigid-body-dynamics simulator for robotics that prioritizes physical accuracy and differentiability: Dojo. The simulator utilizes an expressive maximal-coordinates representation, achieves stable simulation at low sample rates, and conserves energy and momentum by employing a variational integrator. A nonlinear complementarity problem, with nonlinear friction cones, models hard contact and is reliably solved using a custom primal-dual interior-point method. The implicit-function theorem enables efficient differentiation of an intermediate relaxed problem and computes smooth gradients from the contact model. We demonstrate the usefulness of the simulator and its gradients through a number of examples including: simulation, trajectory optimization, reinforcement learning, and system identification.

Trajectory Optimization with Optimization-Based Dynamics

We present a framework for bi-level trajectory optimization in which a system's dynamics are encoded as the solution to a constrained optimization problem and smooth gradients of this lower-level problem are passed to an upper-level trajectory optimizer. This optimization-based dynamics representation enables constraint handling, additional variables, and non-smooth forces to be abstracted away from the upper-level optimizer, and allows classical unconstrained optimizers to synthesize trajectories for more complex systems. We provide a path-following method for efficient evaluation of constrained dynamics and utilize the implicit-function theorem to compute smooth gradients of this representation. We demonstrate the framework by modeling systems from locomotion, aerospace, and manipulation domains including: acrobot with joint limits, cart-pole subject to Coulomb friction, Raibert hopper, rocket landing with thrust limits, and planar-push task with optimization-based dynamics and then optimize trajectories using iterative LQR.

Direct Policy Optimization using Deterministic Sampling and Collocation

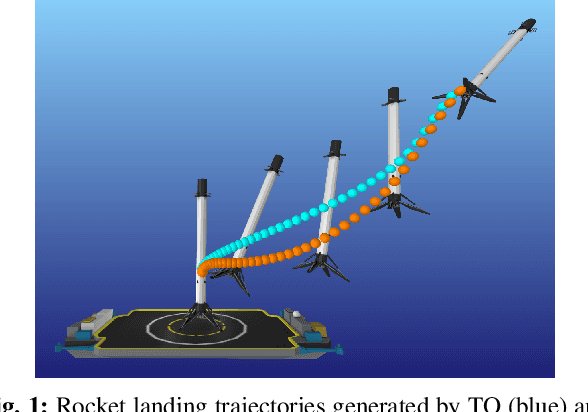
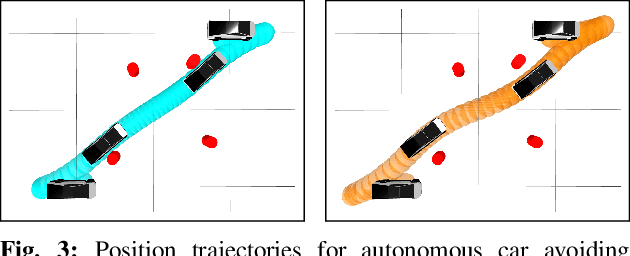
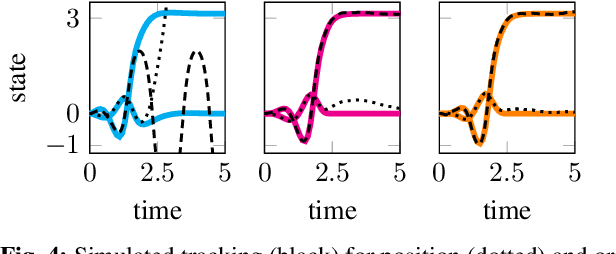
We present an approach for approximately solving discrete-time stochastic optimal control problems by combining direct trajectory optimization, deterministic sampling, and policy optimization. Our feedback motion planning algorithm uses a quasi-Newton method to simultaneously optimize a nominal trajectory, a set of deterministically chosen sample trajectories, and a parameterized policy. We demonstrate that this approach exactly recovers LQR policies in the case of linear dynamics, quadratic cost, and Gaussian noise. We also demonstrate the algorithm on several nonlinear, underactuated robotic systems to highlight its performance and ability to handle control limits, safely avoid obstacles, and generate robust plans in the presence of unmodeled dynamics.