Direct Policy Optimization using Deterministic Sampling and Collocation

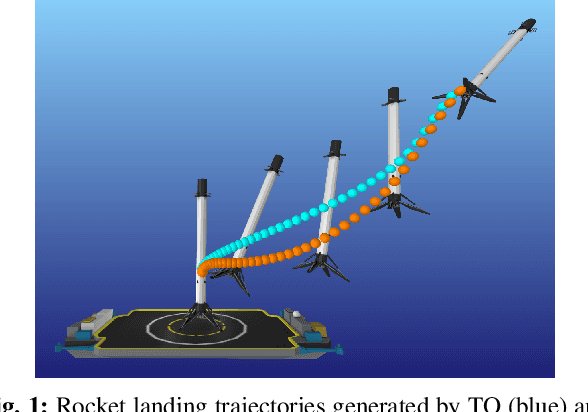
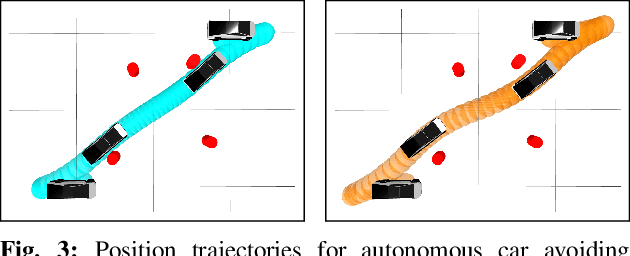
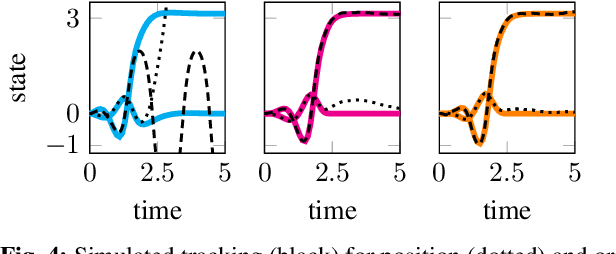
We present an approach for approximately solving discrete-time stochastic optimal control problems by combining direct trajectory optimization, deterministic sampling, and policy optimization. Our feedback motion planning algorithm uses a quasi-Newton method to simultaneously optimize a nominal trajectory, a set of deterministically chosen sample trajectories, and a parameterized policy. We demonstrate that this approach exactly recovers LQR policies in the case of linear dynamics, quadratic cost, and Gaussian noise. We also demonstrate the algorithm on several nonlinear, underactuated robotic systems to highlight its performance and ability to handle control limits, safely avoid obstacles, and generate robust plans in the presence of unmodeled dynamics.