Direct Policy Optimization using Deterministic Sampling and Collocation

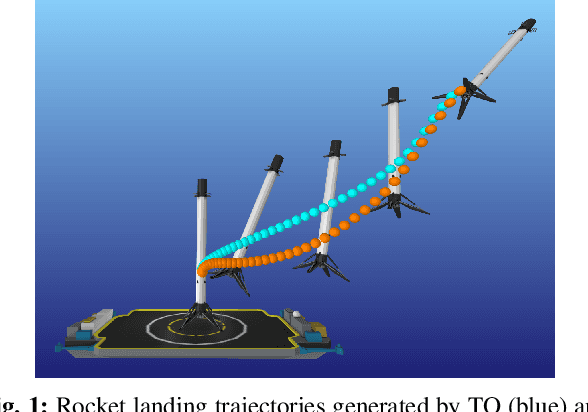
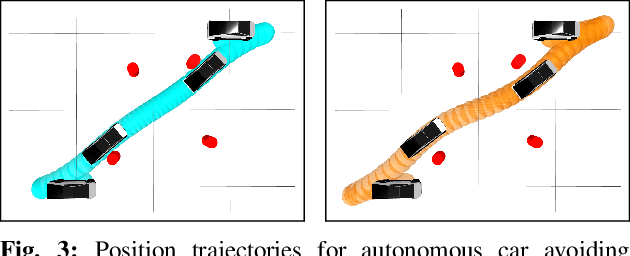
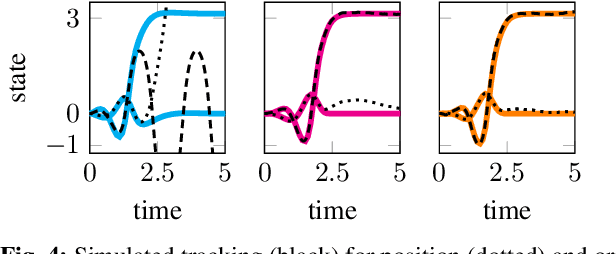
We present an approach for approximately solving discrete-time stochastic optimal control problems by combining direct trajectory optimization, deterministic sampling, and policy optimization. Our feedback motion planning algorithm uses a quasi-Newton method to simultaneously optimize a nominal trajectory, a set of deterministically chosen sample trajectories, and a parameterized policy. We demonstrate that this approach exactly recovers LQR policies in the case of linear dynamics, quadratic cost, and Gaussian noise. We also demonstrate the algorithm on several nonlinear, underactuated robotic systems to highlight its performance and ability to handle control limits, safely avoid obstacles, and generate robust plans in the presence of unmodeled dynamics.

Extending iLQR method with control delay

Iterative linear quadradic regulator(iLQR) has become a benchmark method to deal with nonlinear stochastic optimal control problem. However, it does not apply to delay system. In this paper, we extend the iLQR theory and prove new theorem in case of input signal with fixed delay. Which could be beneficial for machine learning or optimal control application to real time robot or human assistive device.