Efficient Online Learning of Contact Force Models for Connector Insertion

Contact-rich manipulation tasks with stiff frictional elements like connector insertion are difficult to model with rigid-body simulators. In this work, we propose a new approach for modeling these environments by learning a quasi-static contact force model instead of a full simulator. Using a feature vector that contains information about the configuration and control, we find a linear mapping adequately captures the relationship between this feature vector and the sensed contact forces. A novel Linear Model Learning (LML) algorithm is used to solve for the globally optimal mapping in real time without any matrix inversions, resulting in an algorithm that runs in nearly constant time on a GPU as the model size increases. We validate the proposed approach for connector insertion both in simulation and hardware experiments, where the learned model is combined with an optimization-based controller to achieve smooth insertions in the presence of misalignments and uncertainty. Our website featuring videos, code, and more materials is available at https://model-based-plugging.github.io/.

ReLU-QP: A GPU-Accelerated Quadratic Programming Solver for Model-Predictive Control

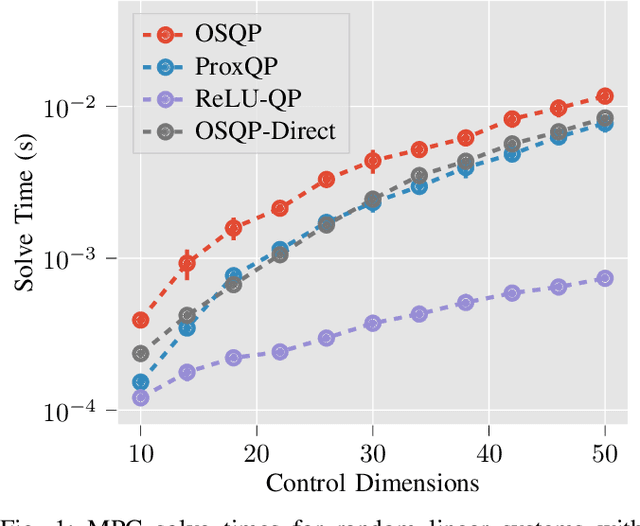
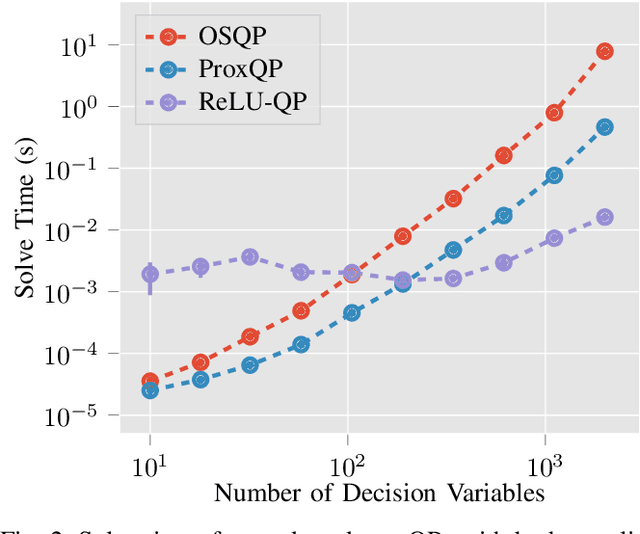
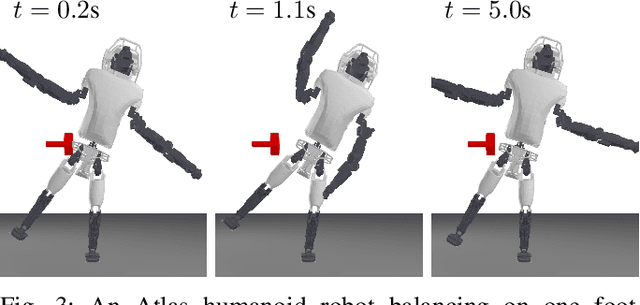
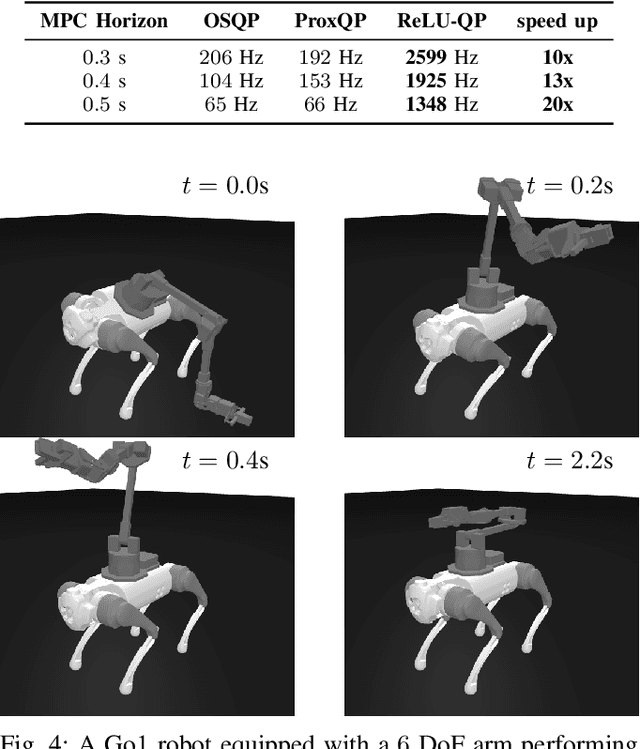
We present ReLU-QP, a GPU-accelerated solver for quadratic programs (QPs) that is capable of solving high-dimensional control problems at real-time rates. ReLU-QP is derived by exactly reformulating the Alternating Direction Method of Multipliers (ADMM) algorithm for solving QPs as a deep, weight-tied neural network with rectified linear unit (ReLU) activations. This reformulation enables the deployment of ReLU-QP on GPUs using standard machine-learning toolboxes. We evaluate the performance of ReLU-QP across three model-predictive control (MPC) benchmarks: stabilizing random linear dynamical systems with control limits, balancing an Atlas humanoid robot on a single foot, and tracking whole-body reference trajectories on a quadruped equipped with a six-degree-of-freedom arm. These benchmarks indicate that ReLU-QP is competitive with state-of-the-art CPU-based solvers for small-to-medium-scale problems and offers order-of-magnitude speed improvements for larger-scale problems.

A Square-Root Kalman Filter Using Only QR Decompositions

The Kalman filter operates by storing a Gaussian description of the state estimate in the form of a mean and covariance. Instead of storing and manipulating the covariance matrix directly, a square-root Kalman filter only forms and updates a triangular matrix square root of the covariance matrix. The resulting algorithm is more numerically stable than a traditional Kalman filter, benefiting from double the working precision. This paper presents a formulation of the square root Kalman filter that leverages the QR decomposition to dramatically simplify the resulting algorithm.

Differentiable Collision Detection for a Set of Convex Primitives

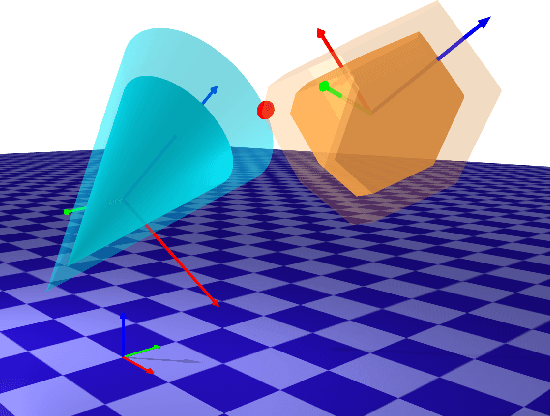
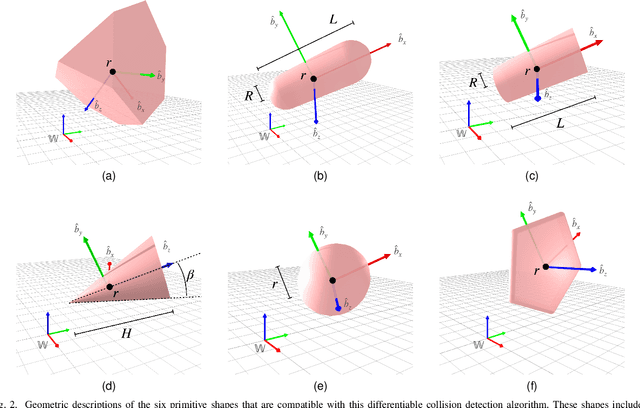
Collision detection between objects is critical for simulation, control, and learning for robotic systems. However, existing collision detection routines are inherently non-differentiable, limiting their usefulness in optimization-based algorithms. In this work, we propose a fully differentiable collision-detection framework that reasons about distances between a set of composable and highly expressive convex primitive shapes. This is achieved by formulating the collision detection problem as a convex optimization problem that seeks to find the minimum uniform scaling to be applied to each object before there is an intersection. The optimization problem is fully differentiable and is able to return both the collision detection status as well as the contact points on each object.

DiffPills: Differentiable Collision Detection for Capsules and Padded Polygons

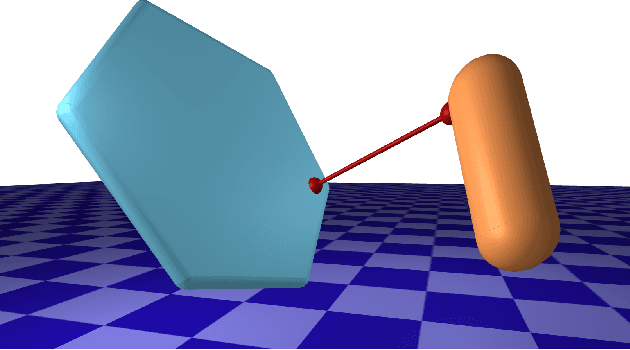
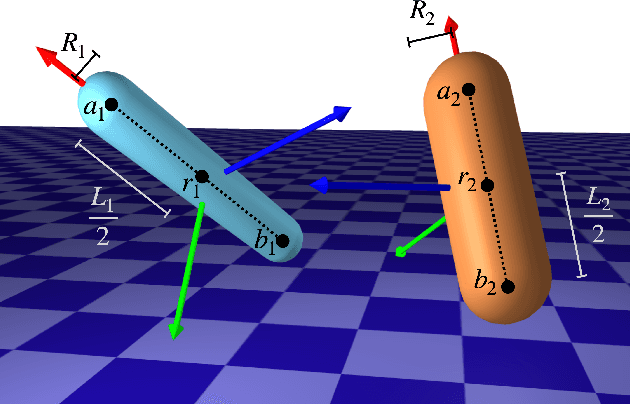
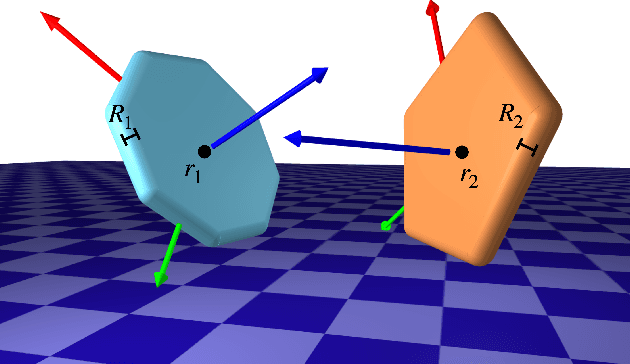
Collision detection plays an important role in simulation, control, and learning for robotic systems. However, no existing method is differentiable with respect to the configurations of the objects, greatly limiting the sort of algorithms that can be built on top of collision detection. In this work, we propose a set of differentiable collision detection algorithms between capsules and padded polygons by formulating these problems as differentiable convex quadratic programs. The resulting algorithms are able to return a proximity value indicating if a collision has taken place, as well as the closest points between objects, all of which are differentiable. As a result, they can be used reliably within other gradient-based optimization methods, including trajectory optimization, state estimation, and reinforcement learning methods.

CALIPSO: A Differentiable Solver for Trajectory Optimization with Conic and Complementarity Constraints

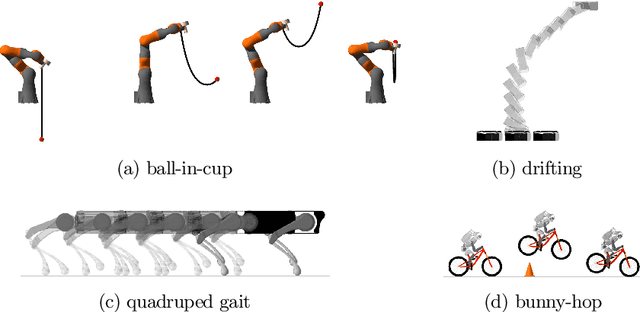
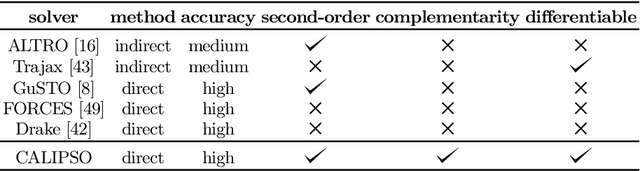
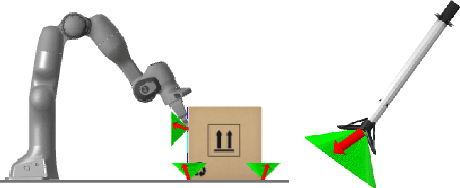
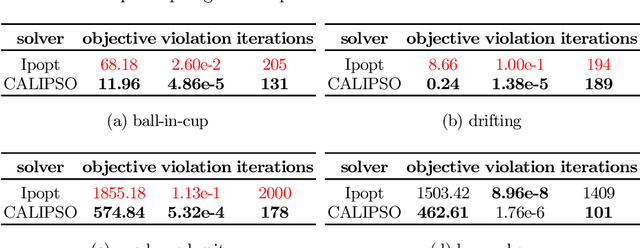
We present a new solver for non-convex trajectory optimization problems that is specialized for robotics applications. CALIPSO, or the Conic Augmented Lagrangian Interior-Point SOlver, combines several strategies for constrained numerical optimization to natively handle second-order cones and complementarity constraints. It reliably solves challenging motion-planning problems that include contact-implicit formulations of impacts and Coulomb friction, thrust limits subject to conic constraints, and state-triggered constraints where general-purpose nonlinear programming solvers like SNOPT and Ipopt fail to converge. Additionally, CALIPSO supports efficient differentiation of solutions with respect to problem data, enabling bi-level optimization applications like auto-tuning of feedback policies. Reliable convergence of the solver is demonstrated on a range of problems from manipulation, locomotion, and aerospace domains. An open-source implementation of this solver is available.