ReLU-QP: A GPU-Accelerated Quadratic Programming Solver for Model-Predictive Control
Paper and Code
Nov 29, 2023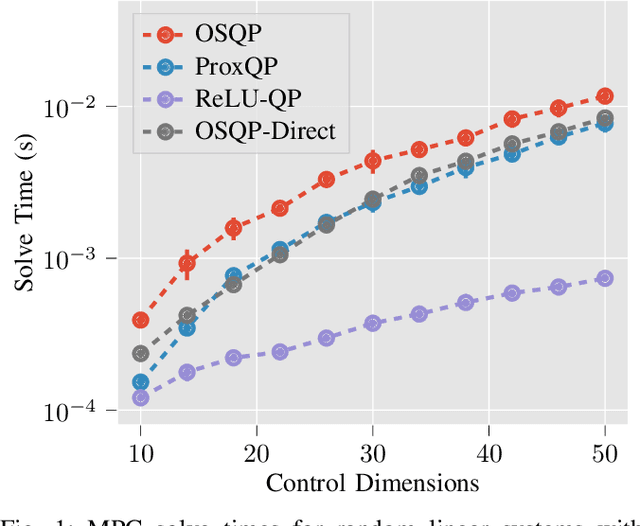
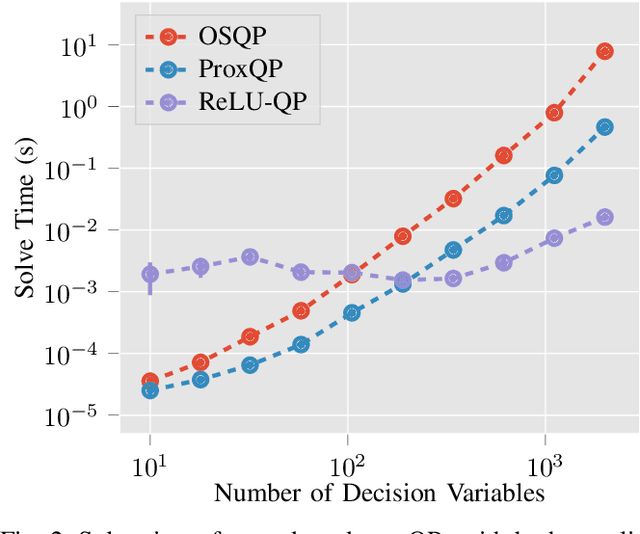
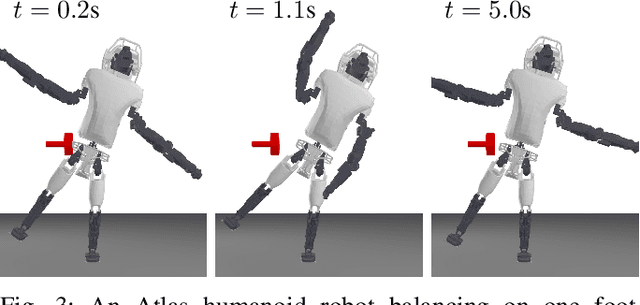
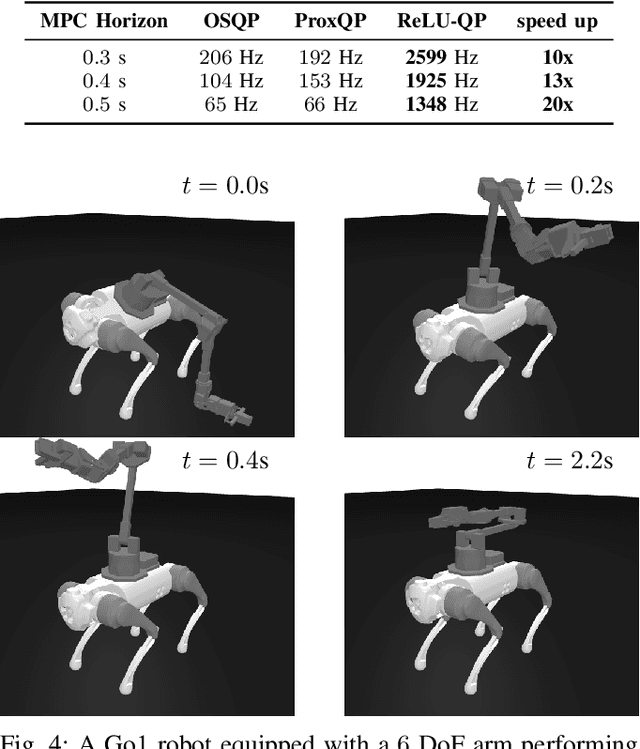
We present ReLU-QP, a GPU-accelerated solver for quadratic programs (QPs) that is capable of solving high-dimensional control problems at real-time rates. ReLU-QP is derived by exactly reformulating the Alternating Direction Method of Multipliers (ADMM) algorithm for solving QPs as a deep, weight-tied neural network with rectified linear unit (ReLU) activations. This reformulation enables the deployment of ReLU-QP on GPUs using standard machine-learning toolboxes. We evaluate the performance of ReLU-QP across three model-predictive control (MPC) benchmarks: stabilizing random linear dynamical systems with control limits, balancing an Atlas humanoid robot on a single foot, and tracking whole-body reference trajectories on a quadruped equipped with a six-degree-of-freedom arm. These benchmarks indicate that ReLU-QP is competitive with state-of-the-art CPU-based solvers for small-to-medium-scale problems and offers order-of-magnitude speed improvements for larger-scale problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge