The Forecast Critic: Leveraging Large Language Models for Poor Forecast Identification

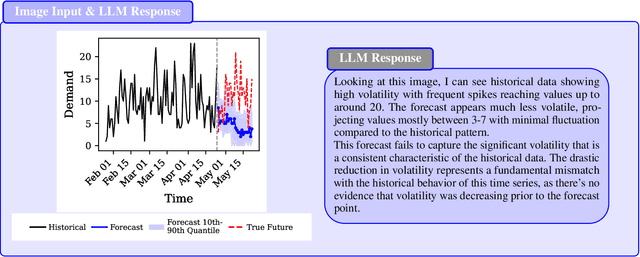
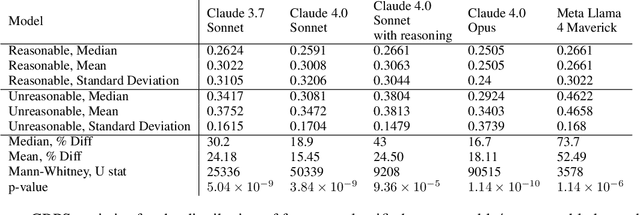
Monitoring forecasting systems is critical for customer satisfaction, profitability, and operational efficiency in large-scale retail businesses. We propose The Forecast Critic, a system that leverages Large Language Models (LLMs) for automated forecast monitoring, taking advantage of their broad world knowledge and strong ``reasoning'' capabilities. As a prerequisite for this, we systematically evaluate the ability of LLMs to assess time series forecast quality, focusing on three key questions. (1) Can LLMs be deployed to perform forecast monitoring and identify obviously unreasonable forecasts? (2) Can LLMs effectively incorporate unstructured exogenous features to assess what a reasonable forecast looks like? (3) How does performance vary across model sizes and reasoning capabilities, measured across state-of-the-art LLMs? We present three experiments, including on both synthetic and real-world forecasting data. Our results show that LLMs can reliably detect and critique poor forecasts, such as those plagued by temporal misalignment, trend inconsistencies, and spike errors. The best-performing model we evaluated achieves an F1 score of 0.88, somewhat below human-level performance (F1 score: 0.97). We also demonstrate that multi-modal LLMs can effectively incorporate unstructured contextual signals to refine their assessment of the forecast. Models correctly identify missing or spurious promotional spikes when provided with historical context about past promotions (F1 score: 0.84). Lastly, we demonstrate that these techniques succeed in identifying inaccurate forecasts on the real-world M5 time series dataset, with unreasonable forecasts having an sCRPS at least 10% higher than that of reasonable forecasts. These findings suggest that LLMs, even without domain-specific fine-tuning, may provide a viable and scalable option for automated forecast monitoring and evaluation.

Stabilization of nonlinear systems with unknown delays via delay-adaptive neural operator approximate predictors

This work establishes the first rigorous stability guarantees for approximate predictors in delay-adaptive control of nonlinear systems, addressing a key challenge in practical implementations where exact predictors are unavailable. We analyze two scenarios: (i) when the actuated input is directly measurable, and (ii) when it is estimated online. For the measurable input case, we prove semi-global practical asymptotic stability with an explicit bound proportional to the approximation error $\epsilon$. For the unmeasured input case, we demonstrate local practical asymptotic stability, with the region of attraction explicitly dependent on both the initial delay estimate and the predictor approximation error. To bridge theory and practice, we show that neural operators-a flexible class of neural network-based approximators-can achieve arbitrarily small approximation errors, thus satisfying the conditions of our stability theorems. Numerical experiments on two nonlinear benchmark systems-a biological protein activator/repressor model and a micro-organism growth Chemostat model-validate our theoretical results. In particular, our numerical simulations confirm stability under approximate predictors, highlight the strong generalization capabilities of neural operators, and demonstrate a substantial computational speedup of up to 15x compared to a baseline fixed-point method.

Neural Operators for Predictor Feedback Control of Nonlinear Delay Systems

Predictor feedback designs are critical for delay-compensating controllers in nonlinear systems. However, these designs are limited in practical applications as predictors cannot be directly implemented, but require numerical approximation schemes. These numerical schemes, typically combining finite difference and successive approximations, become computationally prohibitive when the dynamics of the system are expensive to compute. To alleviate this issue, we propose approximating the predictor mapping via a neural operator. In particular, we introduce a new perspective on predictor designs by recasting the predictor formulation as an operator learning problem. We then prove the existence of an arbitrarily accurate neural operator approximation of the predictor operator. Under the approximated-predictor, we achieve semiglobal practical stability of the closed-loop nonlinear system. The estimate is semiglobal in a unique sense - namely, one can increase the set of initial states as large as desired but this will naturally increase the difficulty of training a neural operator approximation which appears practically in the stability estimate. Furthermore, we emphasize that our result holds not just for neural operators, but any black-box predictor satisfying a universal approximation error bound. From a computational perspective, the advantage of the neural operator approach is clear as it requires training once, offline and then is deployed with very little computational cost in the feedback controller. We conduct experiments controlling a 5-link robotic manipulator with different state-of-the-art neural operator architectures demonstrating speedups on the magnitude of $10^2$ compared to traditional predictor approximation schemes.

Generalizable Motion Planning via Operator Learning

In this work, we introduce a planning neural operator (PNO) for predicting the value function of a motion planning problem. We recast value function approximation as learning a single operator from the cost function space to the value function space, which is defined by an Eikonal partial differential equation (PDE). Specifically, we recast computing value functions as learning a single operator across continuous function spaces which prove is equivalent to solving an Eikonal PDE. Through this reformulation, our learned PNO is able to generalize to new motion planning problems without retraining. Therefore, our PNO model, despite being trained with a finite number of samples at coarse resolution, inherits the zero-shot super-resolution property of neural operators. We demonstrate accurate value function approximation at 16 times the training resolution on the MovingAI lab's 2D city dataset and compare with state-of-the-art neural value function predictors on 3D scenes from the iGibson building dataset. Lastly, we investigate employing the value function output of PNO as a heuristic function to accelerate motion planning. We show theoretically that the PNO heuristic is $\epsilon$-consistent by introducing an inductive bias layer that guarantees our value functions satisfy the triangle inequality. With our heuristic, we achieve a 30% decrease in nodes visited while obtaining near optimal path lengths on the MovingAI lab 2D city dataset, compared to classical planning methods (A*, RRT*).

Adaptive control of reaction-diffusion PDEs via neural operator-approximated gain kernels

Neural operator approximations of the gain kernels in PDE backstepping has emerged as a viable method for implementing controllers in real time. With such an approach, one approximates the gain kernel, which maps the plant coefficient into the solution of a PDE, with a neural operator. It is in adaptive control that the benefit of the neural operator is realized, as the kernel PDE solution needs to be computed online, for every updated estimate of the plant coefficient. We extend the neural operator methodology from adaptive control of a hyperbolic PDE to adaptive control of a benchmark parabolic PDE (a reaction-diffusion equation with a spatially-varying and unknown reaction coefficient). We prove global stability and asymptotic regulation of the plant state for a Lyapunov design of parameter adaptation. The key technical challenge of the result is handling the 2D nature of the gain kernels and proving that the target system with two distinct sources of perturbation terms, due to the parameter estimation error and due to the neural approximation error, is Lyapunov stable. To verify our theoretical result, we present simulations achieving calculation speedups up to 45x relative to the traditional finite difference solvers for every timestep in the simulation trajectory.

PDE Control Gym: A Benchmark for Data-Driven Boundary Control of Partial Differential Equations

Over the last decade, data-driven methods have surged in popularity, emerging as valuable tools for control theory. As such, neural network approximations of control feedback laws, system dynamics, and even Lyapunov functions have attracted growing attention. With the ascent of learning based control, the need for accurate, fast, and easy-to-use benchmarks has increased. In this work, we present the first learning-based environment for boundary control of PDEs. In our benchmark, we introduce three foundational PDE problems - a 1D transport PDE, a 1D reaction-diffusion PDE, and a 2D Navier-Stokes PDE - whose solvers are bundled in an user-friendly reinforcement learning gym. With this gym, we then present the first set of model-free, reinforcement learning algorithms for solving this series of benchmark problems, achieving stability, although at a higher cost compared to model-based PDE backstepping. With the set of benchmark environments and detailed examples, this work significantly lowers the barrier to entry for learning-based PDE control - a topic largely unexplored by the data-driven control community. The entire benchmark is available on Github along with detailed documentation and the presented reinforcement learning models are open sourced.

Adaptive Neural-Operator Backstepping Control of a Benchmark Hyperbolic PDE

To stabilize PDEs, feedback controllers require gain kernel functions, which are themselves governed by PDEs. Furthermore, these gain-kernel PDEs depend on the PDE plants' functional coefficients. The functional coefficients in PDE plants are often unknown. This requires an adaptive approach to PDE control, i.e., an estimation of the plant coefficients conducted concurrently with control, where a separate PDE for the gain kernel must be solved at each timestep upon the update in the plant coefficient function estimate. Solving a PDE at each timestep is computationally expensive and a barrier to the implementation of real-time adaptive control of PDEs. Recently, results in neural operator (NO) approximations of functional mappings have been introduced into PDE control, for replacing the computation of the gain kernel with a neural network that is trained, once offline, and reused in real-time for rapid solution of the PDEs. In this paper, we present the first result on applying NOs in adaptive PDE control, presented for a benchmark 1-D hyperbolic PDE with recirculation. We establish global stabilization via Lyapunov analysis, in the plant and parameter error states, and also present an alternative approach, via passive identifiers, which avoids the strong assumptions on kernel differentiability. We then present numerical simulations demonstrating stability and observe speedups up to three orders of magnitude, highlighting the real-time efficacy of neural operators in adaptive control. Our code (Github) is made publicly available for future researchers.

Gain Scheduling with a Neural Operator for a Transport PDE with Nonlinear Recirculation

To stabilize PDE models, control laws require space-dependent functional gains mapped by nonlinear operators from the PDE functional coefficients. When a PDE is nonlinear and its "pseudo-coefficient" functions are state-dependent, a gain-scheduling (GS) nonlinear design is the simplest approach to the design of nonlinear feedback. The GS version of PDE backstepping employs gains obtained by solving a PDE at each value of the state. Performing such PDE computations in real time may be prohibitive. The recently introduced neural operators (NO) can be trained to produce the gain functions, rapidly in real time, for each state value, without requiring a PDE solution. In this paper we introduce NOs for GS-PDE backstepping. GS controllers act on the premise that the state change is slow and, as a result, guarantee only local stability, even for ODEs. We establish local stabilization of hyperbolic PDEs with nonlinear recirculation using both a "full-kernel" approach and the "gain-only" approach to gain operator approximation. Numerical simulations illustrate stabilization and demonstrate speedup by three orders of magnitude over traditional PDE gain-scheduling. Code (Github) for the numerical implementation is published to enable exploration.

Moving-Horizon Estimators for Hyperbolic and Parabolic PDEs in 1-D

Observers for PDEs are themselves PDEs. Therefore, producing real time estimates with such observers is computationally burdensome. For both finite-dimensional and ODE systems, moving-horizon estimators (MHE) are operators whose output is the state estimate, while their inputs are the initial state estimate at the beginning of the horizon as well as the measured output and input signals over the moving time horizon. In this paper we introduce MHEs for PDEs which remove the need for a numerical solution of an observer PDE in real time. We accomplish this using the PDE backstepping method which, for certain classes of both hyperbolic and parabolic PDEs, produces moving-horizon state estimates explicitly. Precisely, to explicitly produce the state estimates, we employ a backstepping transformation of a hard-to-solve observer PDE into a target observer PDE, which is explicitly solvable. The MHEs we propose are not new observer designs but simply the explicit MHE realizations, over a moving horizon of arbitrary length, of the existing backstepping observers. Our PDE MHEs lack the optimality of the MHEs that arose as duals of MPC, but they are given explicitly, even for PDEs. In the paper we provide explicit formulae for MHEs for both hyperbolic and parabolic PDEs, as well as simulation results that illustrate theoretically guaranteed convergence of the MHEs.

Neural Operators of Backstepping Controller and Observer Gain Functions for Reaction-Diffusion PDEs

Unlike ODEs, whose models involve system matrices and whose controllers involve vector or matrix gains, PDE models involve functions in those roles functional coefficients, dependent on the spatial variables, and gain functions dependent on space as well. The designs of gains for controllers and observers for PDEs, such as PDE backstepping, are mappings of system model functions into gain functions. These infinite dimensional nonlinear operators are given in an implicit form through PDEs, in spatial variables, which need to be solved to determine the gain function for each new functional coefficient of the PDE. The need for solving such PDEs can be eliminated by learning and approximating the said design mapping in the form of a neural operator. Learning the neural operator requires a sufficient number of prior solutions for the design PDEs, offline, as well as the training of the operator. In recent work, we developed the neural operators for PDE backstepping designs for first order hyperbolic PDEs. Here we extend this framework to the more complex class of parabolic PDEs. The key theoretical question is whether the controllers are still stabilizing, and whether the observers are still convergent, if they employ the approximate functional gains generated by the neural operator. We provide affirmative answers to these questions, namely, we prove stability in closed loop under gains produced by neural operators. We illustrate the theoretical results with numerical tests and publish our code on github. The neural operators are three orders of magnitude faster in generating gain functions than PDE solvers for such gain functions. This opens up the opportunity for the use of this neural operator methodology in adaptive control and in gain scheduling control for nonlinear PDEs.