Contextual Inverse Optimization: Offline and Online Learning
Paper and Code
Jun 26, 2021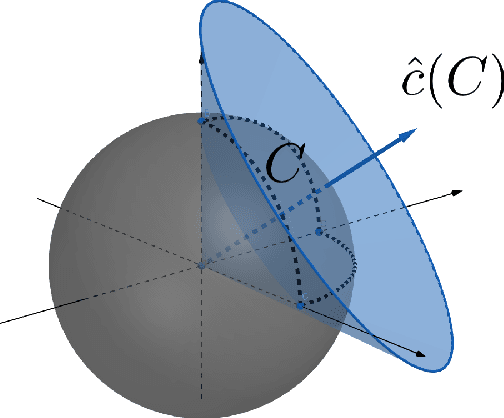

We study the problems of offline and online contextual optimization with feedback information, where instead of observing the loss, we observe, after-the-fact, the optimal action an oracle with full knowledge of the objective function would have taken. We aim to minimize regret, which is defined as the difference between our losses and the ones incurred by an all-knowing oracle. In the offline setting, the decision-maker has information available from past periods and needs to make one decision, while in the online setting, the decision-maker optimizes decisions dynamically over time based a new set of feasible actions and contextual functions in each period. For the offline setting, we characterize the optimal minimax policy, establishing the performance that can be achieved as a function of the underlying geometry of the information induced by the data. In the online setting, we leverage this geometric characterization to optimize the cumulative regret. We develop an algorithm that yields the first regret bound for this problem that is logarithmic in the time horizon.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge