Reinforcement Learning in MDPs with Information-Ordered Policies

We propose an epoch-based reinforcement learning algorithm for infinite-horizon average-cost Markov decision processes (MDPs) that leverages a partial order over a policy class. In this structure, $\pi' \leq \pi$ if data collected under $\pi$ can be used to estimate the performance of $\pi'$, enabling counterfactual inference without additional environment interaction. Leveraging this partial order, we show that our algorithm achieves a regret bound of $O(\sqrt{w \log(|\Theta|) T})$, where $w$ is the width of the partial order. Notably, the bound is independent of the state and action space sizes. We illustrate the applicability of these partial orders in many domains in operations research, including inventory control and queuing systems. For each, we apply our framework to that problem, yielding new theoretical guarantees and strong empirical results without imposing extra assumptions such as convexity in the inventory model or specialized arrival-rate structure in the queuing model.

Auction Design using Value Prediction with Hallucinations

We investigate a Bayesian mechanism design problem where a seller seeks to maximize revenue by selling an indivisible good to one of n buyers, incorporating potentially unreliable predictions (signals) of buyers' private values derived from a machine learning model. We propose a framework where these signals are sometimes reflective of buyers' true valuations but other times are hallucinations, which are uncorrelated with the buyers' true valuations. Our main contribution is a characterization of the optimal auction under this framework. Our characterization establishes a near-decomposition of how to treat types above and below the signal. For the one buyer case, the seller's optimal strategy is to post one of three fairly intuitive prices depending on the signal, which we call the "ignore", "follow" and "cap" actions.

Contextual Inverse Optimization: Offline and Online Learning

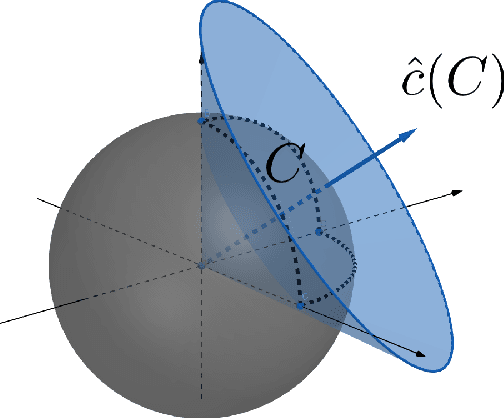
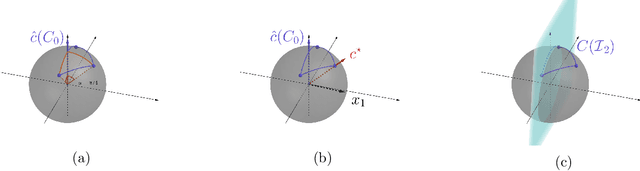
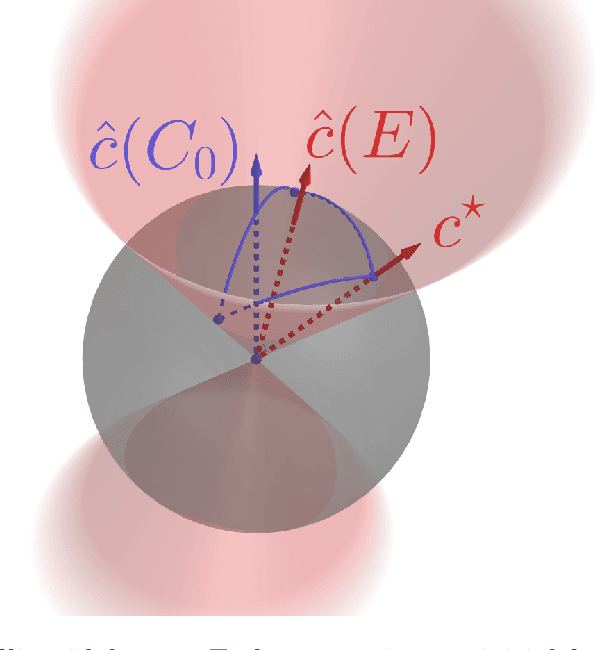
We study the problems of offline and online contextual optimization with feedback information, where instead of observing the loss, we observe, after-the-fact, the optimal action an oracle with full knowledge of the objective function would have taken. We aim to minimize regret, which is defined as the difference between our losses and the ones incurred by an all-knowing oracle. In the offline setting, the decision-maker has information available from past periods and needs to make one decision, while in the online setting, the decision-maker optimizes decisions dynamically over time based a new set of feasible actions and contextual functions in each period. For the offline setting, we characterize the optimal minimax policy, establishing the performance that can be achieved as a function of the underlying geometry of the information induced by the data. In the online setting, we leverage this geometric characterization to optimize the cumulative regret. We develop an algorithm that yields the first regret bound for this problem that is logarithmic in the time horizon.

Multidimensional Binary Search for Contextual Decision-Making

We consider a multidimensional search problem that is motivated by questions in contextual decision-making, such as dynamic pricing and personalized medicine. Nature selects a state from a $d$-dimensional unit ball and then generates a sequence of $d$-dimensional directions. We are given access to the directions, but not access to the state. After receiving a direction, we have to guess the value of the dot product between the state and the direction. Our goal is to minimize the number of times when our guess is more than $\epsilon$ away from the true answer. We construct a polynomial time algorithm that we call Projected Volume achieving regret $O(d\log(d/\epsilon))$, which is optimal up to a $\log d$ factor. The algorithm combines a volume cutting strategy with a new geometric technique that we call cylindrification.