Quantized Distributed Training of Large Models with Convergence Guarantees

Communication-reduction techniques are a popular way to improve scalability in data-parallel training of deep neural networks (DNNs). The recent emergence of large language models such as GPT has created the need for new approaches to exploit data-parallelism. Among these, fully-sharded data parallel (FSDP) training is highly popular, yet it still encounters scalability bottlenecks. One reason is that applying compression techniques to FSDP is challenging: as the vast majority of the communication involves the model's weights, direct compression alters convergence and leads to accuracy loss. We present QSDP, a variant of FSDP which supports both gradient and weight quantization with theoretical guarantees, is simple to implement and has essentially no overheads. To derive QSDP we prove that a natural modification of SGD achieves convergence even when we only maintain quantized weights, and thus the domain over which we train consists of quantized points and is, therefore, highly non-convex. We validate this approach by training GPT-family models with up to 1.3 billion parameters on a multi-node cluster. Experiments show that QSDP preserves model accuracy, while completely removing the communication bottlenecks of FSDP, providing end-to-end speedups of up to 2.2x.

CrAM: A Compression-Aware Minimizer

We examine the question of whether SGD-based optimization of deep neural networks (DNNs) can be adapted to produce models which are both highly-accurate and easily-compressible. We propose a new compression-aware minimizer dubbed CrAM, which modifies the SGD training iteration in a principled way, in order to produce models whose local loss behavior is stable under compression operations such as weight pruning or quantization. Experimental results on standard image classification tasks show that CrAM produces dense models that can be more accurate than standard SGD-type baselines, but which are surprisingly stable under weight pruning: for instance, for ResNet50 on ImageNet, CrAM-trained models can lose up to 70% of their weights in one shot with only minor accuracy loss.

AC/DC: Alternating Compressed/DeCompressed Training of Deep Neural Networks

The increasing computational requirements of deep neural networks (DNNs) have led to significant interest in obtaining DNN models that are sparse, yet accurate. Recent work has investigated the even harder case of sparse training, where the DNN weights are, for as much as possible, already sparse to reduce computational costs during training. Existing sparse training methods are mainly empirical and often have lower accuracy relative to the dense baseline. In this paper, we present a general approach called Alternating Compressed/DeCompressed (AC/DC) training of DNNs, demonstrate convergence for a variant of the algorithm, and show that AC/DC outperforms existing sparse training methods in accuracy at similar computational budgets; at high sparsity levels, AC/DC even outperforms existing methods that rely on accurate pre-trained dense models. An important property of AC/DC is that it allows co-training of dense and sparse models, yielding accurate sparse-dense model pairs at the end of the training process. This is useful in practice, where compressed variants may be desirable for deployment in resource-constrained settings without re-doing the entire training flow, and also provides us with insights into the accuracy gap between dense and compressed models.

Decomposable Submodular Function Minimization via Maximum Flow

This paper bridges discrete and continuous optimization approaches for decomposable submodular function minimization, in both the standard and parametric settings. We provide improved running times for this problem by reducing it to a number of calls to a maximum flow oracle. When each function in the decomposition acts on $O(1)$ elements of the ground set $V$ and is polynomially bounded, our running time is up to polylogarithmic factors equal to that of solving maximum flow in a sparse graph with $O(\vert V \vert)$ vertices and polynomial integral capacities. We achieve this by providing a simple iterative method which can optimize to high precision any convex function defined on the submodular base polytope, provided we can efficiently minimize it on the base polytope corresponding to the cut function of a certain graph that we construct. We solve this minimization problem by lifting the solutions of a parametric cut problem, which we obtain via a new efficient combinatorial reduction to maximum flow. This reduction is of independent interest and implies some previously unknown bounds for the parametric minimum $s,t$-cut problem in multiple settings.

Projection-Free Bandit Optimization with Privacy Guarantees

We design differentially private algorithms for the bandit convex optimization problem in the projection-free setting. This setting is important whenever the decision set has a complex geometry, and access to it is done efficiently only through a linear optimization oracle, hence Euclidean projections are unavailable (e.g. matroid polytope, submodular base polytope). This is the first differentially-private algorithm for projection-free bandit optimization, and in fact our bound of $\widetilde{O}(T^{3/4})$ matches the best known non-private projection-free algorithm (Garber-Kretzu, AISTATS `20) and the best known private algorithm, even for the weaker setting when projections are available (Smith-Thakurta, NeurIPS `13).

Adaptive Gradient Methods for Constrained Convex Optimization

We provide new adaptive first-order methods for constrained convex optimization. Our main algorithms AdaACSA and AdaAGD+ are accelerated methods, which are universal in the sense that they achieve nearly-optimal convergence rates for both smooth and non-smooth functions, even when they only have access to stochastic gradients. In addition, they do not require any prior knowledge on how the objective function is parametrized, since they automatically adjust their per-coordinate learning rate. These can be seen as truly accelerated Adagrad methods for constrained optimization. We complement them with a simpler algorithm AdaGrad+ which enjoys the same features, and achieves the standard non-accelerated convergence rate. We also present a set of new results involving adaptive methods for unconstrained optimization and monotone operators.

A Parallel Double Greedy Algorithm for Submodular Maximization

We study parallel algorithms for the problem of maximizing a non-negative submodular function. Our main result is an algorithm that achieves a nearly-optimal $1/2 -\epsilon$ approximation using $O(\log(1/\epsilon) / \epsilon)$ parallel rounds of function evaluations. Our algorithm is based on a continuous variant of the double greedy algorithm of Buchbinder et al. that achieves the optimal $1/2$ approximation in the sequential setting. Our algorithm applies more generally to the problem of maximizing a continuous diminishing-returns (DR) function.

Towards Deep Learning Models Resistant to Adversarial Attacks

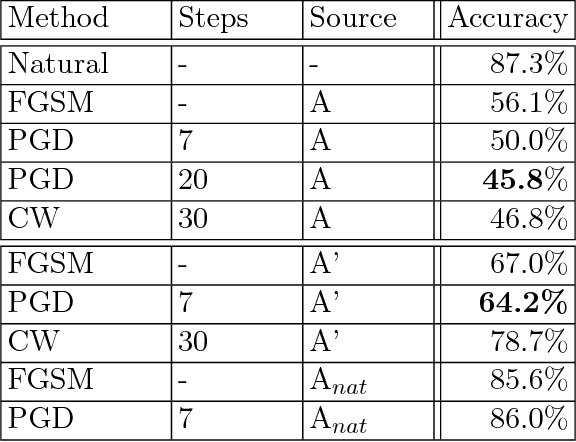
Recent work has demonstrated that neural networks are vulnerable to adversarial examples, i.e., inputs that are almost indistinguishable from natural data and yet classified incorrectly by the network. In fact, some of the latest findings suggest that the existence of adversarial attacks may be an inherent weakness of deep learning models. To address this problem, we study the adversarial robustness of neural networks through the lens of robust optimization. This approach provides us with a broad and unifying view on much of the prior work on this topic. Its principled nature also enables us to identify methods for both training and attacking neural networks that are reliable and, in a certain sense, universal. In particular, they specify a concrete security guarantee that would protect against any adversary. These methods let us train networks with significantly improved resistance to a wide range of adversarial attacks. They also suggest the notion of security against a first-order adversary as a natural and broad security guarantee. We believe that robustness against such well-defined classes of adversaries is an important stepping stone towards fully resistant deep learning models.

Multidimensional Binary Search for Contextual Decision-Making

We consider a multidimensional search problem that is motivated by questions in contextual decision-making, such as dynamic pricing and personalized medicine. Nature selects a state from a $d$-dimensional unit ball and then generates a sequence of $d$-dimensional directions. We are given access to the directions, but not access to the state. After receiving a direction, we have to guess the value of the dot product between the state and the direction. Our goal is to minimize the number of times when our guess is more than $\epsilon$ away from the true answer. We construct a polynomial time algorithm that we call Projected Volume achieving regret $O(d\log(d/\epsilon))$, which is optimal up to a $\log d$ factor. The algorithm combines a volume cutting strategy with a new geometric technique that we call cylindrification.

Tight Bounds for Approximate Carathéodory and Beyond

We give a deterministic nearly-linear time algorithm for approximating any point inside a convex polytope with a sparse convex combination of the polytope's vertices. Our result provides a constructive proof for the Approximate Carath\'{e}odory Problem, which states that any point inside a polytope contained in the $\ell_p$ ball of radius $D$ can be approximated to within $\epsilon$ in $\ell_p$ norm by a convex combination of only $O\left(D^2 p/\epsilon^2\right)$ vertices of the polytope for $p \geq 2$. We also show that this bound is tight, using an argument based on anti-concentration for the binomial distribution. Along the way of establishing the upper bound, we develop a technique for minimizing norms over convex sets with complicated geometry; this is achieved by running Mirror Descent on a dual convex function obtained via Sion's Theorem. As simple extensions of our method, we then provide new algorithms for submodular function minimization and SVM training. For submodular function minimization we obtain a simplification and (provable) speed-up over Wolfe's algorithm, the method commonly found to be the fastest in practice. For SVM training, we obtain $O(1/\epsilon^2)$ convergence for arbitrary kernels; each iteration only requires matrix-vector operations involving the kernel matrix, so we overcome the obstacle of having to explicitly store the kernel or compute its Cholesky factorization.