Improved Feature Importance Computations for Tree Models: Shapley vs. Banzhaf

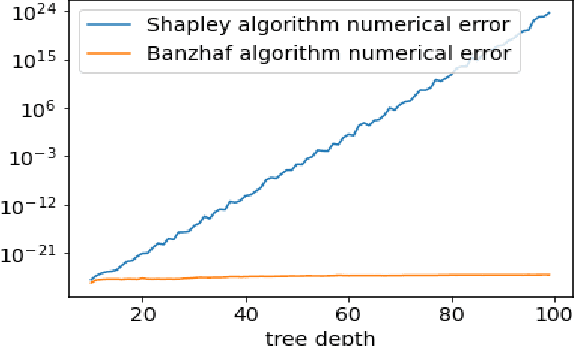
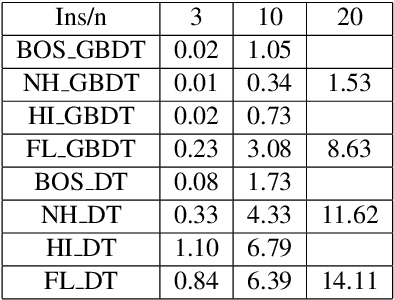
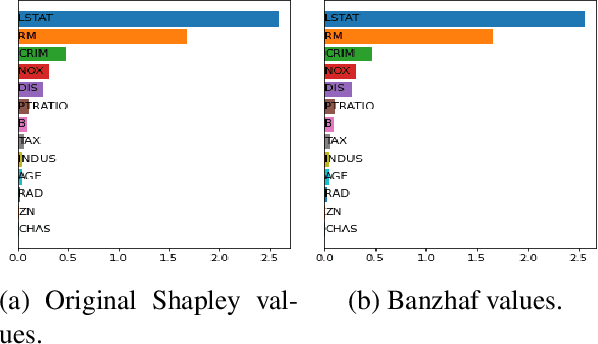
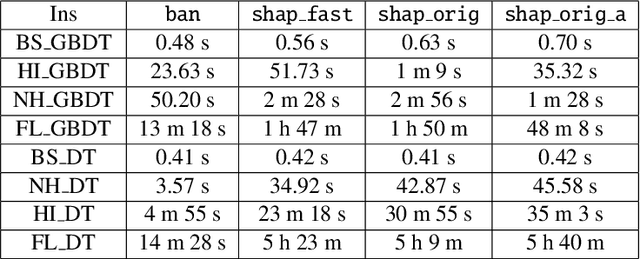
Shapley values are one of the main tools used to explain predictions of tree ensemble models. The main alternative to Shapley values are Banzhaf values that have not been understood equally well. In this paper we make a step towards filling this gap, providing both experimental and theoretical comparison of these model explanation methods. Surprisingly, we show that Banzhaf values offer several advantages over Shapley values while providing essentially the same explanations. We verify that Banzhaf values: (1) have a more intuitive interpretation, (2) allow for more efficient algorithms, and (3) are much more numerically robust. We provide an experimental evaluation of these theses. In particular, we show that on real world instances. Additionally, from a theoretical perspective we provide new and improved algorithm computing the same Shapley value based explanations as the algorithm of Lundberg et al. [Nat. Mach. Intell. 2020]. Our algorithm runs in $O(TLD+n)$ time, whereas the previous algorithm had $O(TLD^2+n)$ running time bound. Here, $T$ is the number of trees, $L$ is the maximum number of leaves in a tree, and $D$ denotes the maximum depth of a tree in the ensemble. Using the computational techniques developed for Shapley values we deliver an optimal $O(TL+n)$ time algorithm for computing Banzhaf values based explanations. In our experiments these algorithms give running times smaller even by an order of magnitude.

Decomposable Submodular Function Minimization via Maximum Flow

This paper bridges discrete and continuous optimization approaches for decomposable submodular function minimization, in both the standard and parametric settings. We provide improved running times for this problem by reducing it to a number of calls to a maximum flow oracle. When each function in the decomposition acts on $O(1)$ elements of the ground set $V$ and is polynomially bounded, our running time is up to polylogarithmic factors equal to that of solving maximum flow in a sparse graph with $O(\vert V \vert)$ vertices and polynomial integral capacities. We achieve this by providing a simple iterative method which can optimize to high precision any convex function defined on the submodular base polytope, provided we can efficiently minimize it on the base polytope corresponding to the cut function of a certain graph that we construct. We solve this minimization problem by lifting the solutions of a parametric cut problem, which we obtain via a new efficient combinatorial reduction to maximum flow. This reduction is of independent interest and implies some previously unknown bounds for the parametric minimum $s,t$-cut problem in multiple settings.

A Novel Minimum Divergence Approach to Robust Speaker Identification

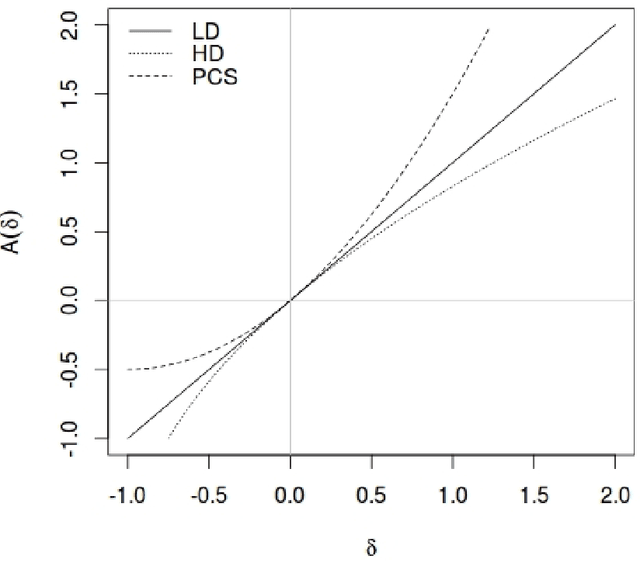
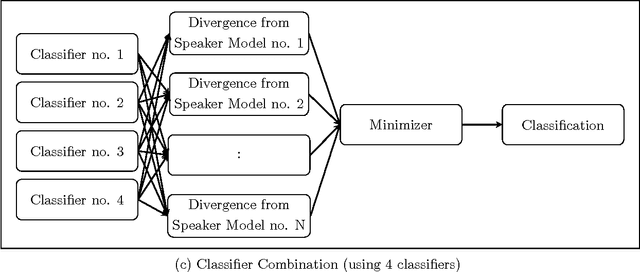
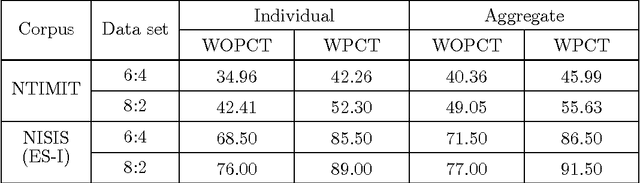
In this work, a novel solution to the speaker identification problem is proposed through minimization of statistical divergences between the probability distribution (g). of feature vectors from the test utterance and the probability distributions of the feature vector corresponding to the speaker classes. This approach is made more robust to the presence of outliers, through the use of suitably modified versions of the standard divergence measures. The relevant solutions to the minimum distance methods are referred to as the minimum rescaled modified distance estimators (MRMDEs). Three measures were considered - the likelihood disparity, the Hellinger distance and Pearson's chi-square distance. The proposed approach is motivated by the observation that, in the case of the likelihood disparity, when the empirical distribution function is used to estimate g, it becomes equivalent to maximum likelihood classification with Gaussian Mixture Models (GMMs) for speaker classes, a highly effective approach used, for example, by Reynolds [22] based on Mel Frequency Cepstral Coefficients (MFCCs) as features. Significant improvement in classification accuracy is observed under this approach on the benchmark speech corpus NTIMIT and a new bilingual speech corpus NISIS, with MFCC features, both in isolation and in combination with delta MFCC features. Moreover, the ubiquitous principal component transformation, by itself and in conjunction with the principle of classifier combination, is found to further enhance the performance.