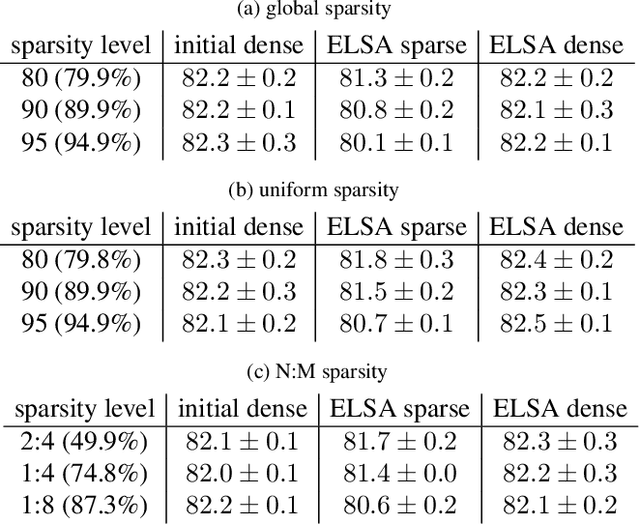
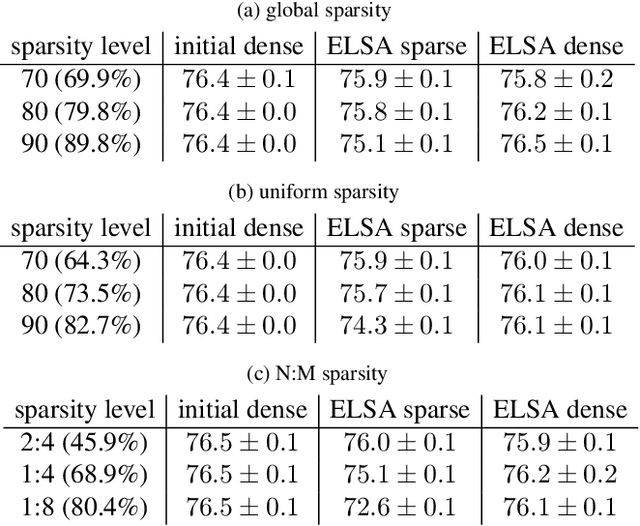
ELSA: Partial Weight Freezing for Overhead-Free Sparse Network Deployment

We present ELSA, a practical solution for creating deep networks that can easily be deployed at different levels of sparsity. The core idea is to embed one or more sparse networks within a single dense network as a proper subset of the weights. At prediction time, any sparse model can be extracted effortlessly simply be zeroing out weights according to a predefined mask. ELSA is simple, powerful and highly flexible. It can use essentially any existing technique for network sparsification and network training. In particular, it does not restrict the loss function, architecture or the optimization technique. Our experiments show that ELSA's advantages of flexible deployment comes with no or just a negligible reduction in prediction quality compared to the standard way of using multiple sparse networks that are trained and stored independently.

Accurate Neural Network Pruning Requires Rethinking Sparse Optimization

Obtaining versions of deep neural networks that are both highly-accurate and highly-sparse is one of the main challenges in the area of model compression, and several high-performance pruning techniques have been investigated by the community. Yet, much less is known about the interaction between sparsity and the standard stochastic optimization techniques used for training sparse networks, and most existing work uses standard dense schedules and hyperparameters for training sparse networks. In this work, we examine the impact of high sparsity on model training using the standard computer vision and natural language processing sparsity benchmarks. We begin by showing that using standard dense training recipes for sparse training is suboptimal, and results in under-training. We provide new approaches for mitigating this issue for both sparse pre-training of vision models (e.g. ResNet50/ImageNet) and sparse fine-tuning of language models (e.g. BERT/GLUE), achieving state-of-the-art results in both settings in the high-sparsity regime, and providing detailed analyses for the difficulty of sparse training in both scenarios. Our work sets a new threshold in terms of the accuracies that can be achieved under high sparsity, and should inspire further research into improving sparse model training, to reach higher accuracies under high sparsity, but also to do so efficiently.

Knowledge Distillation Performs Partial Variance Reduction

Knowledge distillation is a popular approach for enhancing the performance of ``student'' models, with lower representational capacity, by taking advantage of more powerful ``teacher'' models. Despite its apparent simplicity and widespread use, the underlying mechanics behind knowledge distillation (KD) are still not fully understood. In this work, we shed new light on the inner workings of this method, by examining it from an optimization perspective. We show that, in the context of linear and deep linear models, KD can be interpreted as a novel type of stochastic variance reduction mechanism. We provide a detailed convergence analysis of the resulting dynamics, which hold under standard assumptions for both strongly-convex and non-convex losses, showing that KD acts as a form of \emph{partial variance reduction}, which can reduce the stochastic gradient noise, but may not eliminate it completely, depending on the properties of the ``teacher'' model. Our analysis puts further emphasis on the need for careful parametrization of KD, in particular w.r.t. the weighting of the distillation loss, and is validated empirically on both linear models and deep neural networks.

Bias in Pruned Vision Models: In-Depth Analysis and Countermeasures

Pruning - that is, setting a significant subset of the parameters of a neural network to zero - is one of the most popular methods of model compression. Yet, several recent works have raised the issue that pruning may induce or exacerbate bias in the output of the compressed model. Despite existing evidence for this phenomenon, the relationship between neural network pruning and induced bias is not well-understood. In this work, we systematically investigate and characterize this phenomenon in Convolutional Neural Networks for computer vision. First, we show that it is in fact possible to obtain highly-sparse models, e.g. with less than 10% remaining weights, which do not decrease in accuracy nor substantially increase in bias when compared to dense models. At the same time, we also find that, at higher sparsities, pruned models exhibit higher uncertainty in their outputs, as well as increased correlations, which we directly link to increased bias. We propose easy-to-use criteria which, based only on the uncompressed model, establish whether bias will increase with pruning, and identify the samples most susceptible to biased predictions post-compression.

CrAM: A Compression-Aware Minimizer

We examine the question of whether SGD-based optimization of deep neural networks (DNNs) can be adapted to produce models which are both highly-accurate and easily-compressible. We propose a new compression-aware minimizer dubbed CrAM, which modifies the SGD training iteration in a principled way, in order to produce models whose local loss behavior is stable under compression operations such as weight pruning or quantization. Experimental results on standard image classification tasks show that CrAM produces dense models that can be more accurate than standard SGD-type baselines, but which are surprisingly stable under weight pruning: for instance, for ResNet50 on ImageNet, CrAM-trained models can lose up to 70% of their weights in one shot with only minor accuracy loss.

How Well Do Sparse Imagenet Models Transfer?

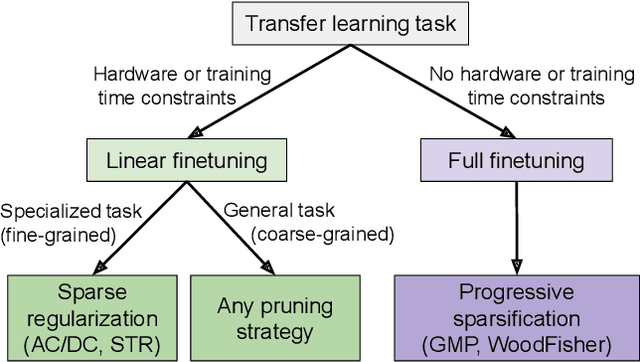
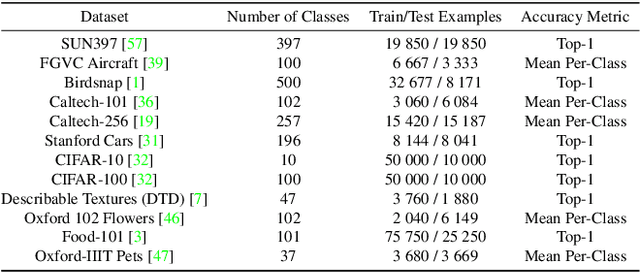
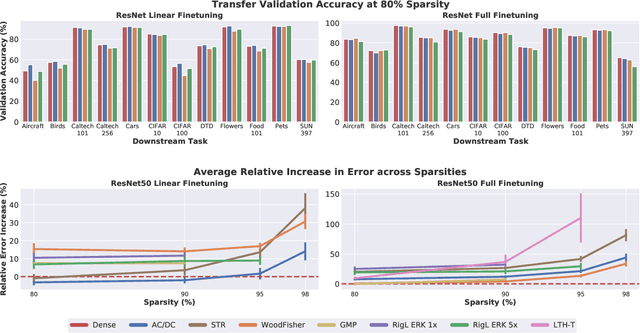
Transfer learning is a classic paradigm by which models pretrained on large "upstream" datasets are adapted to yield good results on "downstream," specialized datasets. Generally, it is understood that more accurate models on the "upstream" dataset will provide better transfer accuracy "downstream". In this work, we perform an in-depth investigation of this phenomenon in the context of convolutional neural networks (CNNs) trained on the ImageNet dataset, which have been pruned - that is, compressed by sparsifiying their connections. Specifically, we consider transfer using unstructured pruned models obtained by applying several state-of-the-art pruning methods, including magnitude-based, second-order, re-growth and regularization approaches, in the context of twelve standard transfer tasks. In a nutshell, our study shows that sparse models can match or even outperform the transfer performance of dense models, even at high sparsities, and, while doing so, can lead to significant inference and even training speedups. At the same time, we observe and analyze significant differences in the behaviour of different pruning methods.

SSSE: Efficiently Erasing Samples from Trained Machine Learning Models

The availability of large amounts of user-provided data has been key to the success of machine learning for many real-world tasks. Recently, an increasing awareness has emerged that users should be given more control about how their data is used. In particular, users should have the right to prohibit the use of their data for training machine learning systems, and to have it erased from already trained systems. While several sample erasure methods have been proposed, all of them have drawbacks which have prevented them from gaining widespread adoption. Most methods are either only applicable to very specific families of models, sacrifice too much of the original model's accuracy, or they have prohibitive memory or computational requirements. In this paper, we propose an efficient and effective algorithm, SSSE, for samples erasure, that is applicable to a wide class of machine learning models. From a second-order analysis of the model's loss landscape we derive a closed-form update step of the model parameters that only requires access to the data to be erased, not to the original training set. Experiments on three datasets, CelebFaces attributes (CelebA), Animals with Attributes 2 (AwA2) and CIFAR10, show that in certain cases SSSE can erase samples almost as well as the optimal, yet impractical, gold standard of training a new model from scratch with only the permitted data.

AC/DC: Alternating Compressed/DeCompressed Training of Deep Neural Networks

The increasing computational requirements of deep neural networks (DNNs) have led to significant interest in obtaining DNN models that are sparse, yet accurate. Recent work has investigated the even harder case of sparse training, where the DNN weights are, for as much as possible, already sparse to reduce computational costs during training. Existing sparse training methods are mainly empirical and often have lower accuracy relative to the dense baseline. In this paper, we present a general approach called Alternating Compressed/DeCompressed (AC/DC) training of DNNs, demonstrate convergence for a variant of the algorithm, and show that AC/DC outperforms existing sparse training methods in accuracy at similar computational budgets; at high sparsity levels, AC/DC even outperforms existing methods that rely on accurate pre-trained dense models. An important property of AC/DC is that it allows co-training of dense and sparse models, yielding accurate sparse-dense model pairs at the end of the training process. This is useful in practice, where compressed variants may be desirable for deployment in resource-constrained settings without re-doing the entire training flow, and also provides us with insights into the accuracy gap between dense and compressed models.

Sparsity in Deep Learning: Pruning and growth for efficient inference and training in neural networks

The growing energy and performance costs of deep learning have driven the community to reduce the size of neural networks by selectively pruning components. Similarly to their biological counterparts, sparse networks generalize just as well, if not better than, the original dense networks. Sparsity can reduce the memory footprint of regular networks to fit mobile devices, as well as shorten training time for ever growing networks. In this paper, we survey prior work on sparsity in deep learning and provide an extensive tutorial of sparsification for both inference and training. We describe approaches to remove and add elements of neural networks, different training strategies to achieve model sparsity, and mechanisms to exploit sparsity in practice. Our work distills ideas from more than 300 research papers and provides guidance to practitioners who wish to utilize sparsity today, as well as to researchers whose goal is to push the frontier forward. We include the necessary background on mathematical methods in sparsification, describe phenomena such as early structure adaptation, the intricate relations between sparsity and the training process, and show techniques for achieving acceleration on real hardware. We also define a metric of pruned parameter efficiency that could serve as a baseline for comparison of different sparse networks. We close by speculating on how sparsity can improve future workloads and outline major open problems in the field.