Incentivized Exploration via Filtered Posterior Sampling

We study "incentivized exploration" (IE) in social learning problems where the principal (a recommendation algorithm) can leverage information asymmetry to incentivize sequentially-arriving agents to take exploratory actions. We identify posterior sampling, an algorithmic approach that is well known in the multi-armed bandits literature, as a general-purpose solution for IE. In particular, we expand the existing scope of IE in several practically-relevant dimensions, from private agent types to informative recommendations to correlated Bayesian priors. We obtain a general analysis of posterior sampling in IE which allows us to subsume these extended settings as corollaries, while also recovering existing results as special cases.

Smoothness-Adaptive Stochastic Bandits

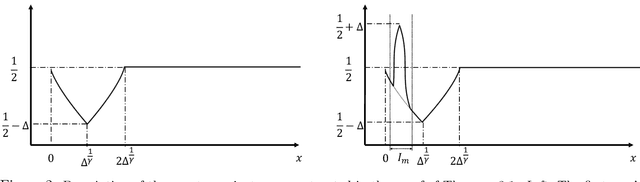
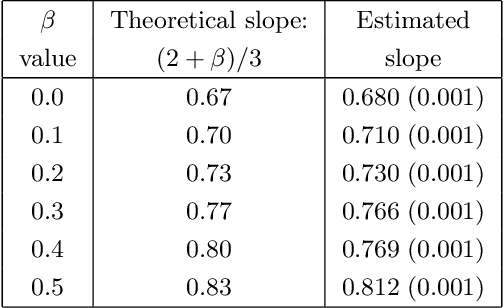
We consider the problem of non-parametric multi-armed bandits with stochastic covariates, where a key factor in determining the complexity of the problem and in the design of effective policies is the smoothness of payoff functions. Previous work treats this problem when the smoothness of payoff functions are a priori known. In practical settings, however, the smoothness that characterizes the class of functions to which payoff functions belong is not known in advance, and misspecification of this smoothness may cause the performance of existing methods to severely deteriorate. In this work, we address the challenge of adapting to a priori unknown smoothness in the payoff functions. Our approach is based on the notion of \textit{self-similarity} that appears in the literature on adaptive non-parametric confidence intervals. We develop a procedure that infers a global smoothness parameter of the payoff functions based on collected observations, and establish that this procedure achieves rate-optimal performance up to logarithmic factors. We further extend this method in order to account for local complexity of the problem which depends on how smooth payoff functions are in different regions of the covariate space. We show that under reasonable assumptions on the way this smoothness changes over the covariate space, our method achieves significantly improved performance that is characterized by the local complexity of the problem as opposed to its global complexity.

Adaptive Sequential Experiments with Unknown Information Flows

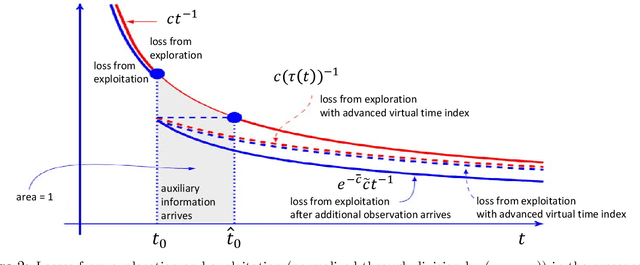
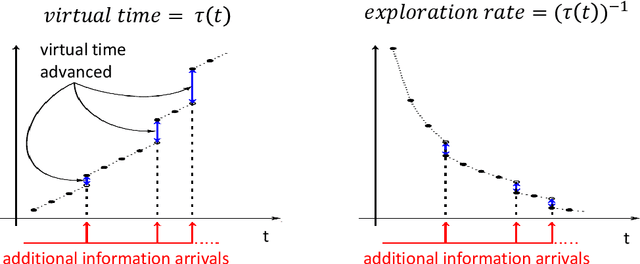
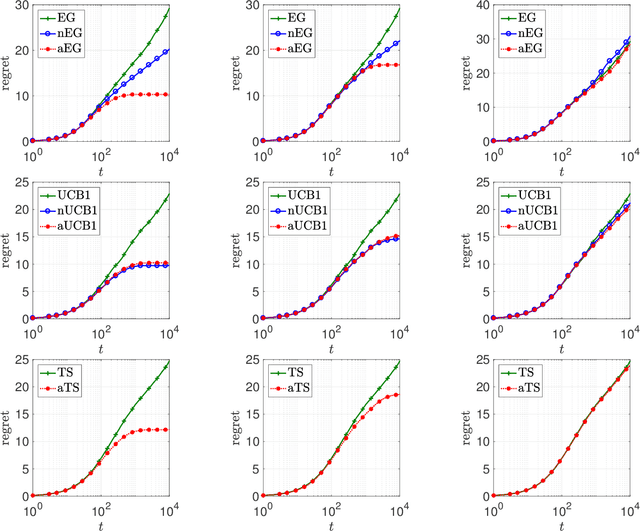
Systems that make sequential decisions in the presence of partial feedback on actions often need to strike a balance between maximizing immediate payoffs based on available information, and acquiring new information that may be essential for maximizing future payoffs. This trade-off is captured by the multi-armed bandit (MAB) framework that has been studied and applied for designing sequential experiments when at each time epoch a single observation is collected on the action that was selected at that epoch. However, in many practical settings additional information may become available between decision epochs. We introduce a generalized MAB formulation in which auxiliary information on each arm may appear arbitrarily over time. By obtaining matching lower and upper bounds, we characterize the minimax complexity of this family of MAB problems as a function of the information arrival process, and study how salient characteristics of this process impact policy design and achievable performance. We establish the robustness of a Thompson sampling policy in the presence of additional information, but observe that other policies that are of practical importance do not exhibit such robustness. We therefore introduce a broad adaptive exploration approach for designing policies that, without any prior knowledge on the information arrival process, attain the best performance (in terms of regret rate) that is achievable when the information arrival process is a priori known. Our approach is based on adjusting MAB policies designed to perform well in the absence of auxiliary information by using dynamically customized virtual time indexes to endogenously control the exploration rate of the policy. We demonstrate our approach through appropriately adjusting known MAB policies and establishing improved performance bounds for these policies in the presence of auxiliary information.

Optimal Exploration-Exploitation in a Multi-Armed-Bandit Problem with Non-stationary Rewards

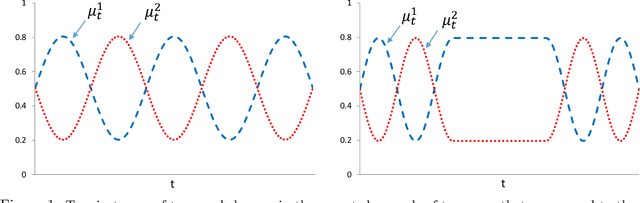
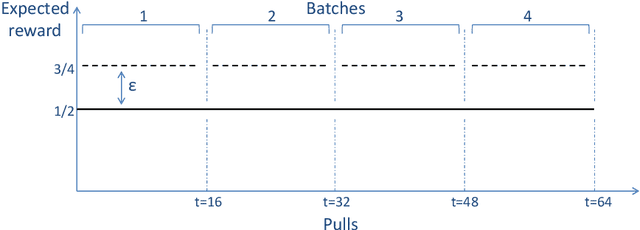
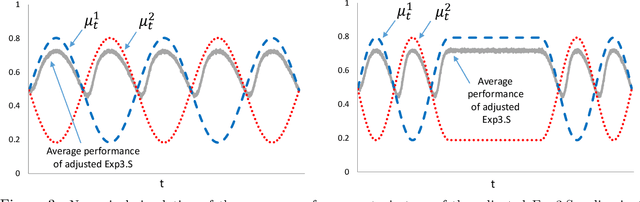
In a multi-armed bandit (MAB) problem a gambler needs to choose at each round of play one of K arms, each characterized by an unknown reward distribution. Reward realizations are only observed when an arm is selected, and the gambler's objective is to maximize his cumulative expected earnings over some given horizon of play T. To do this, the gambler needs to acquire information about arms (exploration) while simultaneously optimizing immediate rewards (exploitation); the price paid due to this trade off is often referred to as the regret, and the main question is how small can this price be as a function of the horizon length T. This problem has been studied extensively when the reward distributions do not change over time; an assumption that supports a sharp characterization of the regret, yet is often violated in practical settings. In this paper, we focus on a MAB formulation which allows for a broad range of temporal uncertainties in the rewards, while still maintaining mathematical tractability. We fully characterize the (regret) complexity of this class of MAB problems by establishing a direct link between the extent of allowable reward "variation" and the minimal achievable regret. Our analysis draws some connections between two rather disparate strands of literature: the adversarial and the stochastic MAB frameworks.