Adaptive Sequential Experiments with Unknown Information Flows

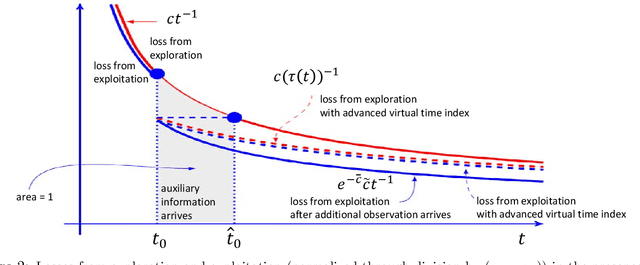
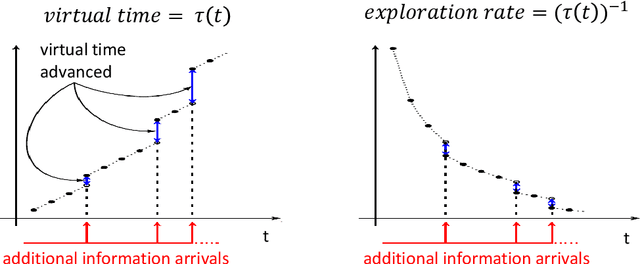
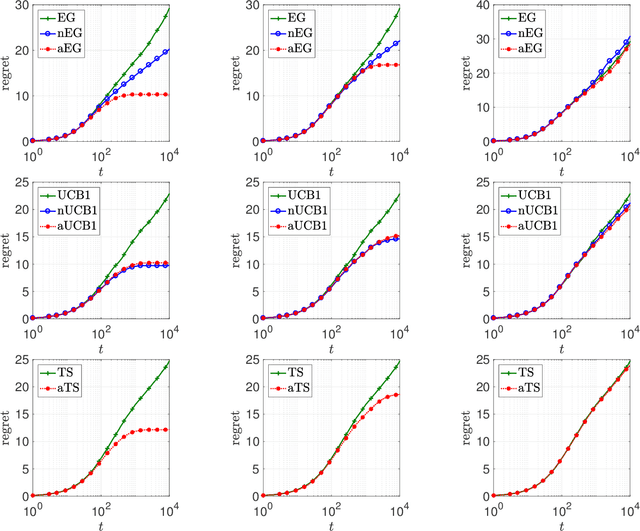
Systems that make sequential decisions in the presence of partial feedback on actions often need to strike a balance between maximizing immediate payoffs based on available information, and acquiring new information that may be essential for maximizing future payoffs. This trade-off is captured by the multi-armed bandit (MAB) framework that has been studied and applied for designing sequential experiments when at each time epoch a single observation is collected on the action that was selected at that epoch. However, in many practical settings additional information may become available between decision epochs. We introduce a generalized MAB formulation in which auxiliary information on each arm may appear arbitrarily over time. By obtaining matching lower and upper bounds, we characterize the minimax complexity of this family of MAB problems as a function of the information arrival process, and study how salient characteristics of this process impact policy design and achievable performance. We establish the robustness of a Thompson sampling policy in the presence of additional information, but observe that other policies that are of practical importance do not exhibit such robustness. We therefore introduce a broad adaptive exploration approach for designing policies that, without any prior knowledge on the information arrival process, attain the best performance (in terms of regret rate) that is achievable when the information arrival process is a priori known. Our approach is based on adjusting MAB policies designed to perform well in the absence of auxiliary information by using dynamically customized virtual time indexes to endogenously control the exploration rate of the policy. We demonstrate our approach through appropriately adjusting known MAB policies and establishing improved performance bounds for these policies in the presence of auxiliary information.