Smoothness-Adaptive Stochastic Bandits

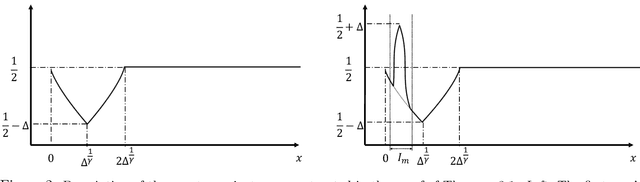
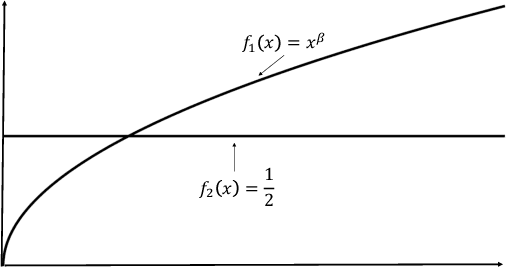
We consider the problem of non-parametric multi-armed bandits with stochastic covariates, where a key factor in determining the complexity of the problem and in the design of effective policies is the smoothness of payoff functions. Previous work treats this problem when the smoothness of payoff functions are a priori known. In practical settings, however, the smoothness that characterizes the class of functions to which payoff functions belong is not known in advance, and misspecification of this smoothness may cause the performance of existing methods to severely deteriorate. In this work, we address the challenge of adapting to a priori unknown smoothness in the payoff functions. Our approach is based on the notion of \textit{self-similarity} that appears in the literature on adaptive non-parametric confidence intervals. We develop a procedure that infers a global smoothness parameter of the payoff functions based on collected observations, and establish that this procedure achieves rate-optimal performance up to logarithmic factors. We further extend this method in order to account for local complexity of the problem which depends on how smooth payoff functions are in different regions of the covariate space. We show that under reasonable assumptions on the way this smoothness changes over the covariate space, our method achieves significantly improved performance that is characterized by the local complexity of the problem as opposed to its global complexity.