C-Learner: Constrained Learning for Causal Inference and Semiparametric Statistics

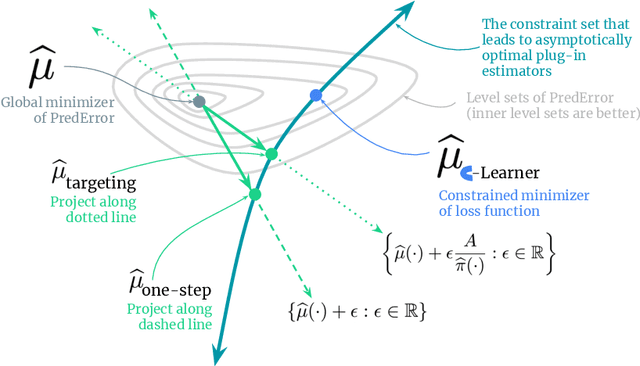
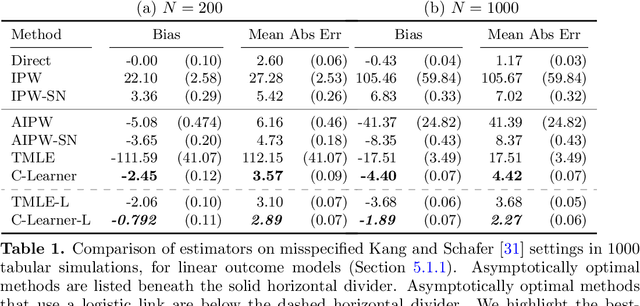
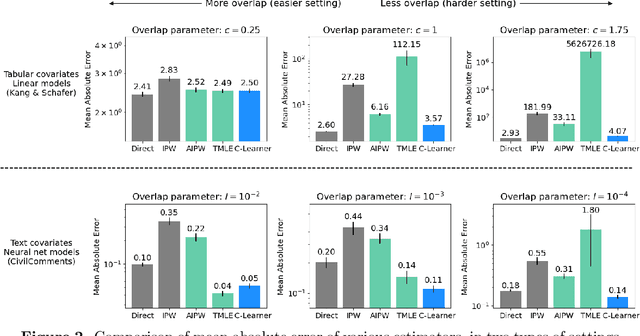
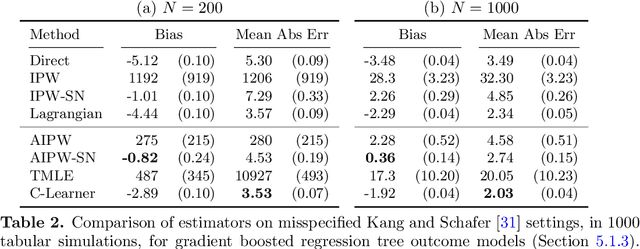
Causal estimation (e.g. of the average treatment effect) requires estimating complex nuisance parameters (e.g. outcome models). To adjust for errors in nuisance parameter estimation, we present a novel correction method that solves for the best plug-in estimator under the constraint that the first-order error of the estimator with respect to the nuisance parameter estimate is zero. Our constrained learning framework provides a unifying perspective to prominent first-order correction approaches including one-step estimation (a.k.a. augmented inverse probability weighting) and targeting (a.k.a. targeted maximum likelihood estimation). Our semiparametric inference approach, which we call the "C-Learner", can be implemented with modern machine learning methods such as neural networks and tree ensembles, and enjoys standard guarantees like semiparametric efficiency and double robustness. Empirically, we demonstrate our approach on several datasets, including those with text features that require fine-tuning language models. We observe the C-Learner matches or outperforms other asymptotically optimal estimators, with better performance in settings with less estimated overlap.

Constrained Learning for Causal Inference and Semiparametric Statistics

Causal estimation (e.g. of the average treatment effect) requires estimating complex nuisance parameters (e.g. outcome models). To adjust for errors in nuisance parameter estimation, we present a novel correction method that solves for the best plug-in estimator under the constraint that the first-order error of the estimator with respect to the nuisance parameter estimate is zero. Our constrained learning framework provides a unifying perspective to prominent first-order correction approaches including debiasing (a.k.a. augmented inverse probability weighting) and targeting (a.k.a. targeted maximum likelihood estimation). Our semiparametric inference approach, which we call the "C-Learner", can be implemented with modern machine learning methods such as neural networks and tree ensembles, and enjoys standard guarantees like semiparametric efficiency and double robustness. Empirically, we demonstrate our approach on several datasets, including those with text features that require fine-tuning language models. We observe the C-Learner matches or outperforms other asymptotically optimal estimators, with better performance in settings with less estimated overlap.

Geometry-Aware Normalizing Wasserstein Flows for Optimal Causal Inference

This manuscript enriches the framework of continuous normalizing flows (CNFs) within causal inference, primarily to augment the geometric properties of parametric submodels used in targeted maximum likelihood estimation (TMLE). By introducing an innovative application of CNFs, we construct a refined series of parametric submodels that enable a directed interpolation between the prior distribution $p_0$ and the empirical distribution $p_1$. This proposed methodology serves to optimize the semiparametric efficiency bound in causal inference by orchestrating CNFs to align with Wasserstein gradient flows. Our approach not only endeavors to minimize the mean squared error in the estimation but also imbues the estimators with geometric sophistication, thereby enhancing robustness against misspecification. This robustness is crucial, as it alleviates the dependence on the standard $n^{\frac{1}{4}}$ rate for a doubly-robust perturbation direction in TMLE. By incorporating robust optimization principles and differential geometry into the estimators, the developed geometry-aware CNFs represent a significant advancement in the pursuit of doubly robust causal inference.

Adaptive Bayesian Learning with Action and State-Dependent Signal Variance

This manuscript presents an advanced framework for Bayesian learning by incorporating action and state-dependent signal variances into decision-making models. This framework is pivotal in understanding complex data-feedback loops and decision-making processes in various economic systems. Through a series of examples, we demonstrate the versatility of this approach in different contexts, ranging from simple Bayesian updating in stable environments to complex models involving social learning and state-dependent uncertainties. The paper uniquely contributes to the understanding of the nuanced interplay between data, actions, outcomes, and the inherent uncertainty in economic models.

Spectral Regularization: an Inductive Bias for Sequence Modeling

Various forms of regularization in learning tasks strive for different notions of simplicity. This paper presents a spectral regularization technique, which attaches a unique inductive bias to sequence modeling based on an intuitive concept of simplicity defined in the Chomsky hierarchy. From fundamental connections between Hankel matrices and regular grammars, we propose to use the trace norm of the Hankel matrix, the tightest convex relaxation of its rank, as the spectral regularizer. To cope with the fact that the Hankel matrix is bi-infinite, we propose an unbiased stochastic estimator for its trace norm. Ultimately, we demonstrate experimental results on Tomita grammars, which exhibit the potential benefits of spectral regularization and validate the proposed stochastic estimator.