BooST: Boosting Smooth Trees for Partial Effect Estimation in Nonlinear Regressions

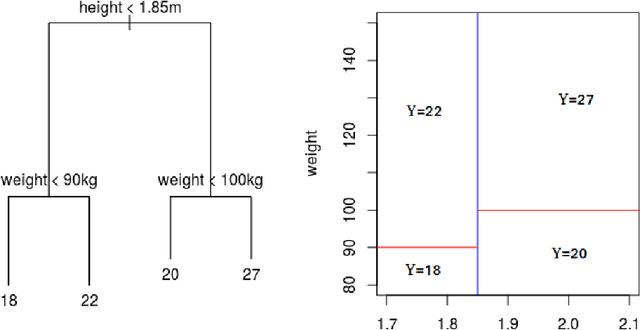
In this paper we introduce a new machine learning (ML) model for nonlinear regression called Boosting Smooth Transition Regression Trees (BooST). The main advantage of the BooST model is that it estimates the derivatives (partial effects) of very general nonlinear models, providing more interpretation about the mapping between the covariates and the dependent variable than other tree based models, such as Random Forests. We provide some asymptotic theory that shows consistency of the partial derivative estimates and we present some examples on both simulated and real data.