Improved Memory-Bounded Dynamic Programming for Decentralized POMDPs
Paper and Code
Jun 20, 2012
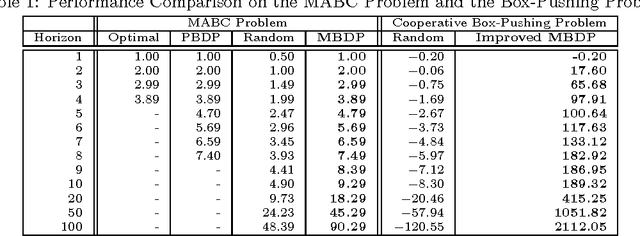
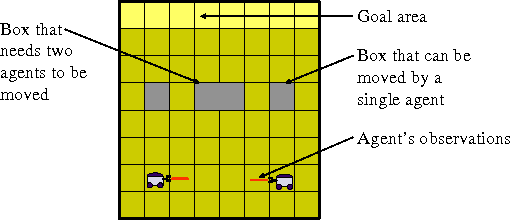
Memory-Bounded Dynamic Programming (MBDP) has proved extremely effective in solving decentralized POMDPs with large horizons. We generalize the algorithm and improve its scalability by reducing the complexity with respect to the number of observations from exponential to polynomial. We derive error bounds on solution quality with respect to this new approximation and analyze the convergence behavior. To evaluate the effectiveness of the improvements, we introduce a new, larger benchmark problem. Experimental results show that despite the high complexity of decentralized POMDPs, scalable solution techniques such as MBDP perform surprisingly well.
* Appears in Proceedings of the Twenty-Third Conference on Uncertainty
in Artificial Intelligence (UAI2007)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge