Tyler Sypherd
Smoothly Giving up: Robustness for Simple Models
Feb 17, 2023



Abstract:There is a growing need for models that are interpretable and have reduced energy and computational cost (e.g., in health care analytics and federated learning). Examples of algorithms to train such models include logistic regression and boosting. However, one challenge facing these algorithms is that they provably suffer from label noise; this has been attributed to the joint interaction between oft-used convex loss functions and simpler hypothesis classes, resulting in too much emphasis being placed on outliers. In this work, we use the margin-based $\alpha$-loss, which continuously tunes between canonical convex and quasi-convex losses, to robustly train simple models. We show that the $\alpha$ hyperparameter smoothly introduces non-convexity and offers the benefit of "giving up" on noisy training examples. We also provide results on the Long-Servedio dataset for boosting and a COVID-19 survey dataset for logistic regression, highlighting the efficacy of our approach across multiple relevant domains.
AugLoss: A Learning Methodology for Real-World Dataset Corruption
Jun 05, 2022
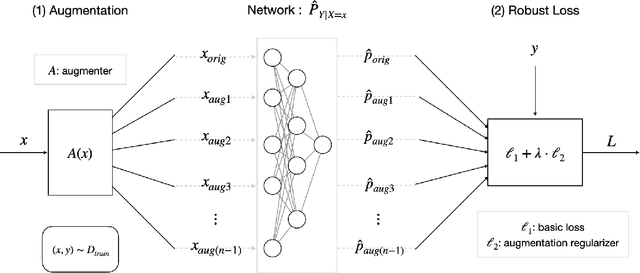
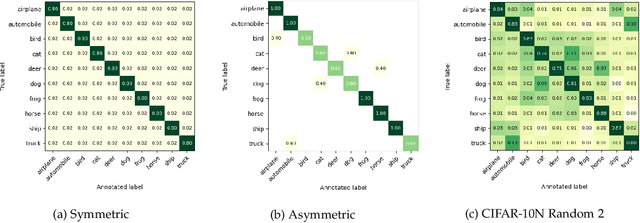
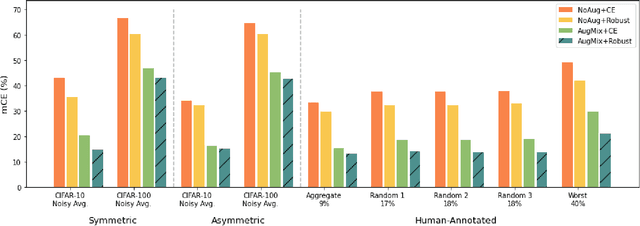
Abstract:Deep Learning (DL) models achieve great successes in many domains. However, DL models increasingly face safety and robustness concerns, including noisy labeling in the training stage and feature distribution shifts in the testing stage. Previous works made significant progress in addressing these problems, but the focus has largely been on developing solutions for only one problem at a time. For example, recent work has argued for the use of tunable robust loss functions to mitigate label noise, and data augmentation (e.g., AugMix) to combat distribution shifts. As a step towards addressing both problems simultaneously, we introduce AugLoss, a simple but effective methodology that achieves robustness against both train-time noisy labeling and test-time feature distribution shifts by unifying data augmentation and robust loss functions. We conduct comprehensive experiments in varied settings of real-world dataset corruption to showcase the gains achieved by AugLoss compared to previous state-of-the-art methods. Lastly, we hope this work will open new directions for designing more robust and reliable DL models under real-world corruptions.
$α$-GAN: Convergence and Estimation Guarantees
May 12, 2022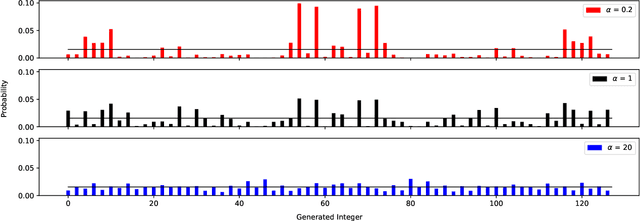

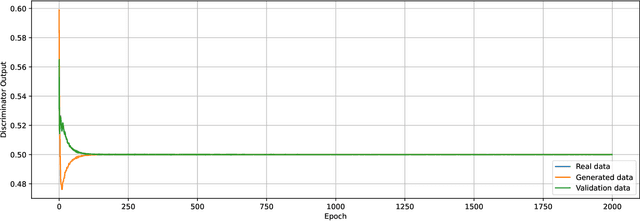

Abstract:We prove a two-way correspondence between the min-max optimization of general CPE loss function GANs and the minimization of associated $f$-divergences. We then focus on $\alpha$-GAN, defined via the $\alpha$-loss, which interpolates several GANs (Hellinger, vanilla, Total Variation) and corresponds to the minimization of the Arimoto divergence. We show that the Arimoto divergences induced by $\alpha$-GAN equivalently converge, for all $\alpha\in \mathbb{R}_{>0}\cup\{\infty\}$. However, under restricted learning models and finite samples, we provide estimation bounds which indicate diverse GAN behavior as a function of $\alpha$. Finally, we present empirical results on a toy dataset that highlight the practical utility of tuning the $\alpha$ hyperparameter.
Being Properly Improper
Jun 18, 2021
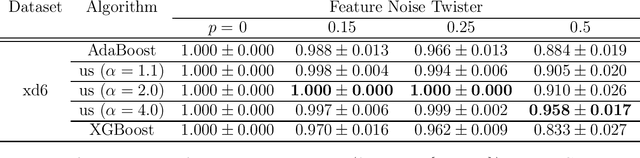


Abstract:In today's ML, data can be twisted (changed) in various ways, either for bad or good intent. Such twisted data challenges the founding theory of properness for supervised losses which form the basis for many popular losses for class probability estimation. Unfortunately, at its core, properness ensures that the optimal models also learn the twist. In this paper, we analyse such class probability-based losses when they are stripped off the mandatory properness; we define twist-proper losses as losses formally able to retrieve the optimum (untwisted) estimate off the twists, and show that a natural extension of a half-century old loss introduced by S. Arimoto is twist proper. We then turn to a theory that has provided some of the best off-the-shelf algorithms for proper losses, boosting. Boosting can require access to the derivative of the convex conjugate of a loss to compute examples weights. Such a function can be hard to get, for computational or mathematical reasons; this turns out to be the case for Arimoto's loss. We bypass this difficulty by inverting the problem as follows: suppose a blueprint boosting algorithm is implemented with a general weight update function. What are the losses for which boosting-compliant minimisation happens? Our answer comes as a general boosting algorithm which meets the optimal boosting dependence on the number of calls to the weak learner; when applied to Arimoto's loss, it leads to a simple optimisation algorithm whose performances are showcased on several domains and twists.
Realizing GANs via a Tunable Loss Function
Jun 09, 2021

Abstract:We introduce a tunable GAN, called $\alpha$-GAN, parameterized by $\alpha \in (0,\infty]$, which interpolates between various $f$-GANs and Integral Probability Metric based GANs (under constrained discriminator set). We construct $\alpha$-GAN using a supervised loss function, namely, $\alpha$-loss, which is a tunable loss function capturing several canonical losses. We show that $\alpha$-GAN is intimately related to the Arimoto divergence, which was first proposed by \"{O}sterriecher (1996), and later studied by Liese and Vajda (2006). We posit that the holistic understanding that $\alpha$-GAN introduces will have practical benefits of addressing both the issues of vanishing gradients and mode collapse.
On the alpha-loss Landscape in the Logistic Model
Jun 22, 2020


Abstract:We analyze the optimization landscape of a recently introduced tunable class of loss functions called $\alpha$-loss, $\alpha \in (0,\infty]$, in the logistic model. This family encapsulates the exponential loss ($\alpha = 1/2$), the log-loss ($\alpha = 1$), and the 0-1 loss ($\alpha = \infty$) and contains compelling properties that enable the practitioner to discern among a host of operating conditions relevant to emerging learning methods. Specifically, we study the evolution of the optimization landscape of $\alpha$-loss with respect to $\alpha$ using tools drawn from the study of strictly-locally-quasi-convex functions in addition to geometric techniques. We interpret these results in terms of optimization complexity via normalized gradient descent.
A Tunable Loss Function for Classification
Jun 26, 2019

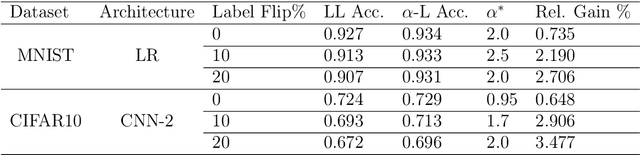

Abstract:Recently, a parametrized class of loss functions called $\alpha$-loss, $\alpha \in [1,\infty]$, has been introduced for classification. This family, which includes the log-loss and the 0-1 loss as special cases, comes with compelling properties including an equivalent margin-based form which is classification-calibrated for all $\alpha$. We introduce a generalization of this family to the entire range of $\alpha \in (0,\infty]$ and establish how the parameter $\alpha$ enables the practitioner to choose among a host of operating conditions that are important in modern machine learning tasks. We prove that smaller $\alpha$ values are more conducive to faster optimization; in fact, $\alpha$-loss is convex for $\alpha \le 1$ and quasi-convex for $\alpha >1$. Moreover, we establish bounds to quantify the degradation of the local-quasi-convexity of the optimization landscape as $\alpha$ increases; we show that this directly translates to a computational slow down. On the other hand, our theoretical results also suggest that larger $\alpha$ values lead to better generalization performance. This is a consequence of the ability of the $\alpha$-loss to limit the effect of less likely data as $\alpha$ increases from 1, thereby facilitating robustness to outliers and noise in the training data. We provide strong evidence supporting this assertion with several experiments on benchmark datasets that establish the efficacy of $\alpha$-loss for $\alpha > 1$ in robustness to errors in the training data. Of equal interest is the fact that, for $\alpha < 1$, our experiments show that the decreased robustness seems to counteract class imbalances in training data.
A Tunable Loss Function for Binary Classification
Mar 19, 2019
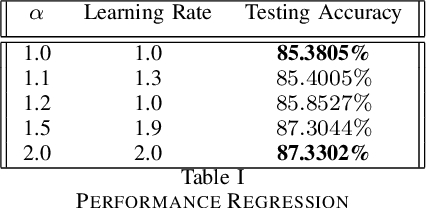
Abstract:We present $\alpha$-loss, $\alpha \in [1,\infty]$, a tunable loss function for binary classification that bridges log-loss ($\alpha=1$) and $0$-$1$ loss ($\alpha = \infty$). We prove that $\alpha$-loss has an equivalent margin-based form and is classification-calibrated, two desirable properties for a good surrogate loss function for the ideal yet intractable $0$-$1$ loss. For logistic regression-based classification, we provide an upper bound on the difference between the empirical and expected risk at the empirical risk minimizers for $\alpha$-loss by exploiting its Lipschitzianity along with recent results on the landscape features of empirical risk functions. Finally, we show that $\alpha$-loss with $\alpha = 2$ performs better than log-loss on MNIST for logistic regression.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge