Theoretical Guarantees of Data Augmented Last Layer Retraining Methods

Ensuring fair predictions across many distinct subpopulations in the training data can be prohibitive for large models. Recently, simple linear last layer retraining strategies, in combination with data augmentation methods such as upweighting, downsampling and mixup, have been shown to achieve state-of-the-art performance for worst-group accuracy, which quantifies accuracy for the least prevalent subpopulation. For linear last layer retraining and the abovementioned augmentations, we present the optimal worst-group accuracy when modeling the distribution of the latent representations (input to the last layer) as Gaussian for each subpopulation. We evaluate and verify our results for both synthetic and large publicly available datasets.

Robustness to Subpopulation Shift with Domain Label Noise via Regularized Annotation of Domains

Existing methods for last layer retraining that aim to optimize worst-group accuracy (WGA) rely heavily on well-annotated groups in the training data. We show, both in theory and practice, that annotation-based data augmentations using either downsampling or upweighting for WGA are susceptible to domain annotation noise, and in high-noise regimes approach the WGA of a model trained with vanilla empirical risk minimization. We introduce Regularized Annotation of Domains (RAD) in order to train robust last layer classifiers without the need for explicit domain annotations. Our results show that RAD is competitive with other recently proposed domain annotation-free techniques. Most importantly, RAD outperforms state-of-the-art annotation-reliant methods even with only 5% noise in the training data for several publicly available datasets.

Addressing GAN Training Instabilities via Tunable Classification Losses

Generative adversarial networks (GANs), modeled as a zero-sum game between a generator (G) and a discriminator (D), allow generating synthetic data with formal guarantees. Noting that D is a classifier, we begin by reformulating the GAN value function using class probability estimation (CPE) losses. We prove a two-way correspondence between CPE loss GANs and $f$-GANs which minimize $f$-divergences. We also show that all symmetric $f$-divergences are equivalent in convergence. In the finite sample and model capacity setting, we define and obtain bounds on estimation and generalization errors. We specialize these results to $\alpha$-GANs, defined using $\alpha$-loss, a tunable CPE loss family parametrized by $\alpha\in(0,\infty]$. We next introduce a class of dual-objective GANs to address training instabilities of GANs by modeling each player's objective using $\alpha$-loss to obtain $(\alpha_D,\alpha_G)$-GANs. We show that the resulting non-zero sum game simplifies to minimizing an $f$-divergence under appropriate conditions on $(\alpha_D,\alpha_G)$. Generalizing this dual-objective formulation using CPE losses, we define and obtain upper bounds on an appropriately defined estimation error. Finally, we highlight the value of tuning $(\alpha_D,\alpha_G)$ in alleviating training instabilities for the synthetic 2D Gaussian mixture ring as well as the large publicly available Celeb-A and LSUN Classroom image datasets.

Towards Addressing GAN Training Instabilities: Dual-objective GANs with Tunable Parameters

In an effort to address the training instabilities of GANs, we introduce a class of dual-objective GANs with different value functions (objectives) for the generator (G) and discriminator (D). In particular, we model each objective using $\alpha$-loss, a tunable classification loss, to obtain $(\alpha_D,\alpha_G)$-GANs, parameterized by $(\alpha_D,\alpha_G)\in [0,\infty)^2$. For sufficiently large number of samples and capacities for G and D, we show that the resulting non-zero sum game simplifies to minimizing an $f$-divergence under appropriate conditions on $(\alpha_D,\alpha_G)$. In the finite sample and capacity setting, we define estimation error to quantify the gap in the generator's performance relative to the optimal setting with infinite samples and obtain upper bounds on this error, showing it to be order optimal under certain conditions. Finally, we highlight the value of tuning $(\alpha_D,\alpha_G)$ in alleviating training instabilities for the synthetic 2D Gaussian mixture ring and the Stacked MNIST datasets.

$α$-GAN: Convergence and Estimation Guarantees

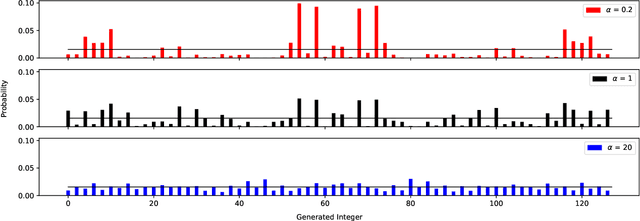
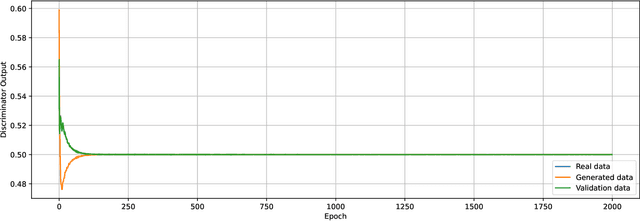
We prove a two-way correspondence between the min-max optimization of general CPE loss function GANs and the minimization of associated $f$-divergences. We then focus on $\alpha$-GAN, defined via the $\alpha$-loss, which interpolates several GANs (Hellinger, vanilla, Total Variation) and corresponds to the minimization of the Arimoto divergence. We show that the Arimoto divergences induced by $\alpha$-GAN equivalently converge, for all $\alpha\in \mathbb{R}_{>0}\cup\{\infty\}$. However, under restricted learning models and finite samples, we provide estimation bounds which indicate diverse GAN behavior as a function of $\alpha$. Finally, we present empirical results on a toy dataset that highlight the practical utility of tuning the $\alpha$ hyperparameter.