Towards Addressing GAN Training Instabilities: Dual-objective GANs with Tunable Parameters
Paper and Code
Feb 28, 2023

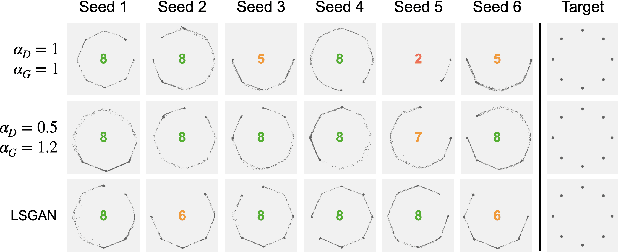

In an effort to address the training instabilities of GANs, we introduce a class of dual-objective GANs with different value functions (objectives) for the generator (G) and discriminator (D). In particular, we model each objective using $\alpha$-loss, a tunable classification loss, to obtain $(\alpha_D,\alpha_G)$-GANs, parameterized by $(\alpha_D,\alpha_G)\in [0,\infty)^2$. For sufficiently large number of samples and capacities for G and D, we show that the resulting non-zero sum game simplifies to minimizing an $f$-divergence under appropriate conditions on $(\alpha_D,\alpha_G)$. In the finite sample and capacity setting, we define estimation error to quantify the gap in the generator's performance relative to the optimal setting with infinite samples and obtain upper bounds on this error, showing it to be order optimal under certain conditions. Finally, we highlight the value of tuning $(\alpha_D,\alpha_G)$ in alleviating training instabilities for the synthetic 2D Gaussian mixture ring and the Stacked MNIST datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge