A Tunable Loss Function for Binary Classification
Paper and Code
Mar 19, 2019
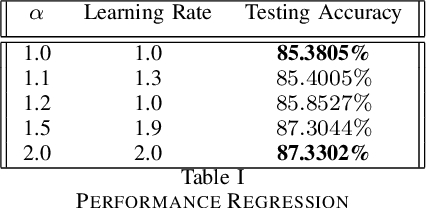
We present $\alpha$-loss, $\alpha \in [1,\infty]$, a tunable loss function for binary classification that bridges log-loss ($\alpha=1$) and $0$-$1$ loss ($\alpha = \infty$). We prove that $\alpha$-loss has an equivalent margin-based form and is classification-calibrated, two desirable properties for a good surrogate loss function for the ideal yet intractable $0$-$1$ loss. For logistic regression-based classification, we provide an upper bound on the difference between the empirical and expected risk at the empirical risk minimizers for $\alpha$-loss by exploiting its Lipschitzianity along with recent results on the landscape features of empirical risk functions. Finally, we show that $\alpha$-loss with $\alpha = 2$ performs better than log-loss on MNIST for logistic regression.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge