To Split or Not to Split: The Impact of Disparate Treatment in Classification

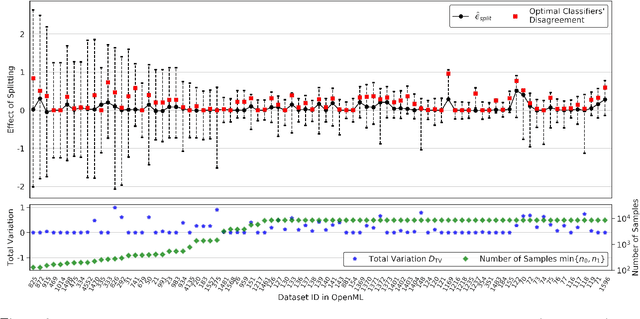
Disparate treatment occurs when a machine learning model produces different decisions for groups defined by a legally protected or sensitive attribute (e.g., race, gender). In domains where prediction accuracy is paramount, it is acceptable to fit a model which exhibits disparate treatment. We explore the effect of splitting classifiers (i.e., training and deploying a separate classifier on each group) and derive an information-theoretic impossibility result: there exists precise conditions where a group-blind classifier will always have a non-trivial performance gap from the split classifiers. We further demonstrate that, in the finite sample regime, splitting is no longer always beneficial and relies on the number of samples from each group and the complexity of the hypothesis class. We provide data-dependent bounds for understanding the effect of splitting and illustrate these bounds on real-world datasets.