Minimax Data Sanitization with Distortion Constraint and Adversarial Inference

We study a privacy-preserving data-sharing setting where a privatizer transforms private data into a sanitized version observed by an authorized reconstructor and two unauthorized adversaries, each with access to side information correlated with the private data. The reconstructor is evaluated under a distortion function, while each adversary is evaluated using a separate loss function. The privatizer ensures the reconstructor distortion remains below a fixed threshold while maximizing the minimum loss across the two adversaries. This two-adversary setting models cases where individual users cannot reconstruct the data accurately, but their combined side information enables estimation within the distortion threshold. The privatizer maximizes individual loss while permitting accurate reconstruction only through collaboration. This echoes secret-sharing principles, but with lossy rather than perfect recovery. We frame this as a constrained data-driven minimax optimization problem and propose a data-driven training procedure that alternately updates the privatizer, reconstructor, and adversaries. We also analyze the Gaussian and binary cases as special scenarios where optimal solutions can be obtained. These theoretical optimal results are benchmarks for evaluating the proposed minimax training approach.

Context-Aware Search and Retrieval Over Erasure Channels

This paper introduces and analyzes a search and retrieval model that adopts key semantic communication principles from retrieval-augmented generation. We specifically present an information-theoretic analysis of a remote document retrieval system operating over a symbol erasure channel. The proposed model encodes the feature vector of a query, derived from term-frequency weights of a language corpus by using a repetition code with an adaptive rate dependent on the contextual importance of the terms. At the decoder, we select between two documents based on the contextual closeness of the recovered query. By leveraging a jointly Gaussian approximation for both the true and reconstructed similarity scores, we derive an explicit expression for the retrieval error probability, i.e., the probability under which the less similar document is selected. Numerical simulations on synthetic and real-world data (Google NQ) confirm the validity of the analysis. They further demonstrate that assigning greater redundancy to critical features effectively reduces the error rate, highlighting the effectiveness of semantic-aware feature encoding in error-prone communication settings.

Differentially-Private Collaborative Online Personalized Mean Estimation

We consider the problem of collaborative personalized mean estimation under a privacy constraint in an environment of several agents continuously receiving data according to arbitrary unknown agent-specific distributions. In particular, we provide a method based on hypothesis testing coupled with differential privacy and data variance estimation. Two privacy mechanisms and two data variance estimation schemes are proposed, and we provide a theoretical convergence analysis of the proposed algorithm for any bounded unknown distributions on the agents' data, showing that collaboration provides faster convergence than a fully local approach where agents do not share data. Moreover, we provide analytical performance curves for the case with an oracle class estimator, i.e., the class structure of the agents, where agents receiving data from distributions with the same mean are considered to be in the same class, is known. The theoretical faster-than-local convergence guarantee is backed up by extensive numerical results showing that for a considered scenario the proposed approach indeed converges much faster than a fully local approach, and performs comparably to ideal performance where all data is public. This illustrates the benefit of private collaboration in an online setting.

VALID: a Validated Algorithm for Learning in Decentralized Networks with Possible Adversarial Presence

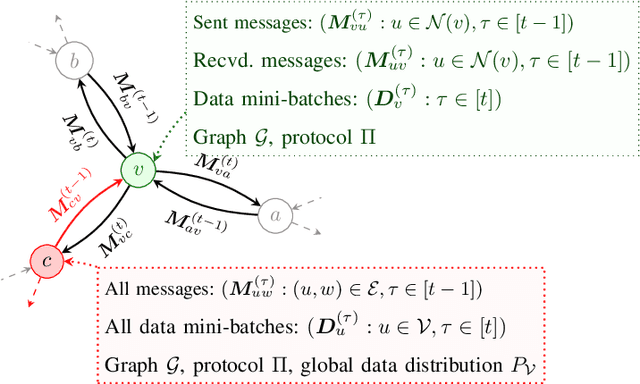
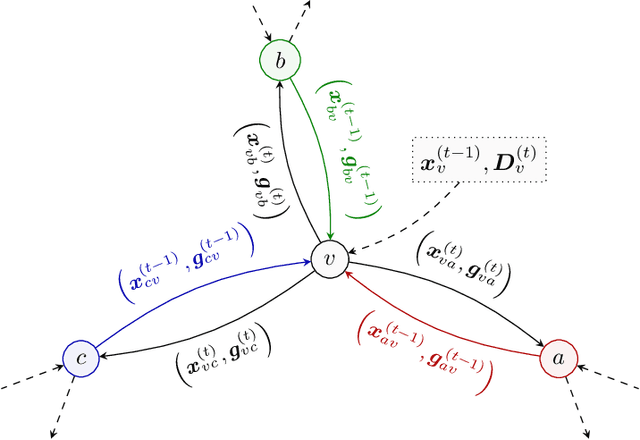
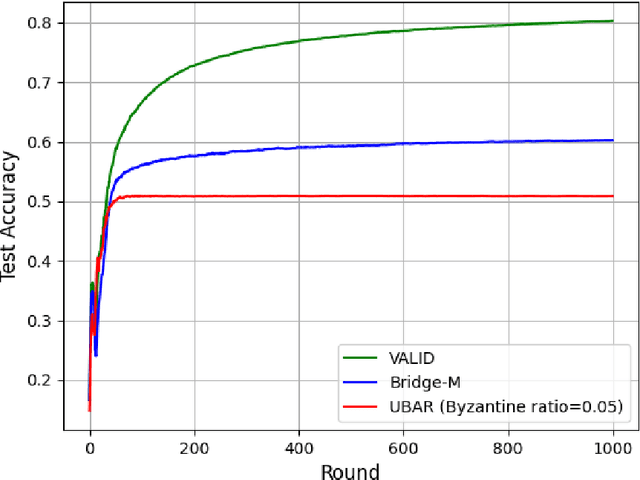
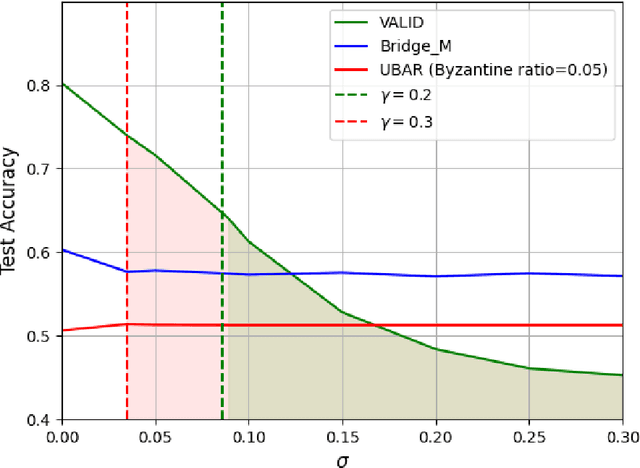
We introduce the paradigm of validated decentralized learning for undirected networks with heterogeneous data and possible adversarial infiltration. We require (a) convergence to a global empirical loss minimizer when adversaries are absent, and (b) either detection of adversarial presence of convergence to an admissible consensus irrespective of the adversarial configuration. To this end, we propose the VALID protocol which, to the best of our knowledge, is the first to achieve a validated learning guarantee. Moreover, VALID offers an O(1/T) convergence rate (under pertinent regularity assumptions), and computational and communication complexities comparable to non-adversarial distributed stochastic gradient descent. Remarkably, VALID retains optimal performance metrics in adversary-free environments, sidestepping the robustness penalties observed in prior byzantine-robust methods. A distinctive aspect of our study is a heterogeneity metric based on the norms of individual agents' gradients computed at the global empirical loss minimizer. This not only provides a natural statistic for detecting significant byzantine disruptions but also allows us to prove the optimality of VALID in wide generality. Lastly, our numerical results reveal that, in the absence of adversaries, VALID converges faster than state-of-the-art byzantine robust algorithms, while when adversaries are present, VALID terminates with each honest either converging to an admissible consensus of declaring adversarial presence in the network.

Straggler-Resilient Differentially-Private Decentralized Learning

We consider the straggler problem in decentralized learning over a logical ring while preserving user data privacy. Especially, we extend the recently proposed framework of differential privacy (DP) amplification by decentralization by Cyffers and Bellet to include overall training latency--comprising both computation and communication latency. Analytical results on both the convergence speed and the DP level are derived for both a skipping scheme (which ignores the stragglers after a timeout) and a baseline scheme that waits for each node to finish before the training continues. A trade-off between overall training latency, accuracy, and privacy, parameterized by the timeout of the skipping scheme, is identified and empirically validated for logistic regression on a real-world dataset.

Generative Adversarial User Privacy in Lossy Single-Server Information Retrieval

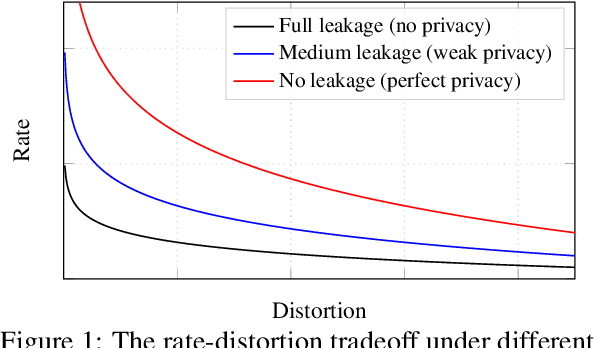
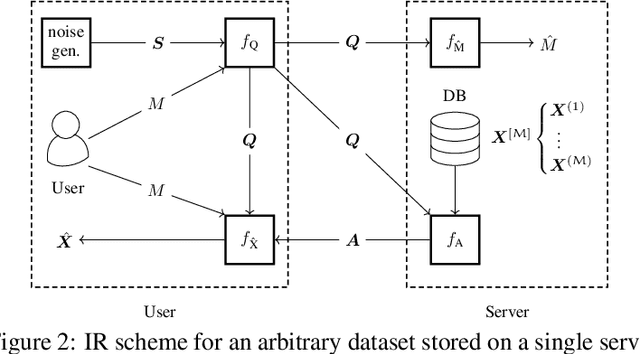
We consider the problem of information retrieval from a dataset of files stored on a single server under both a user distortion and a user privacy constraint. Specifically, a user requesting a file from the dataset should be able to reconstruct the requested file with a prescribed distortion, and in addition, the identity of the requested file should be kept private from the server with a prescribed privacy level. The proposed model can be seen as an extension of the well-known concept of private information retrieval by allowing for distortion in the retrieval process and relaxing the perfect privacy requirement. We initiate the study of the tradeoff between download rate, distortion, and user privacy leakage, and show that the optimal rate-distortion-leakage tradeoff is convex and that in the limit of large file sizes this allows for a concise information-theoretical formulation in terms of mutual information. Moreover, we propose a new data-driven framework by leveraging recent advancements in generative adversarial models which allows a user to learn efficient schemes in terms of download rate from the data itself. Learning the scheme is formulated as a constrained minimax game between a user which desires to keep the identity of the requested file private and an adversary that tries to infer which file the user is interested in under a distortion constraint. In general, guaranteeing a certain privacy level leads to a higher rate-distortion tradeoff curve, and hence a sacrifice in either download rate or distortion. We evaluate the performance of the scheme on a synthetic Gaussian dataset as well as on the MNIST and CIFAR-$10$ datasets. For the MNIST dataset, the data-driven approach significantly outperforms a proposed general achievable scheme combining source coding with the download of multiple files, while for CIFAR-$10$ the performances are comparable.