Differentially-Private Collaborative Online Personalized Mean Estimation

We consider the problem of collaborative personalized mean estimation under a privacy constraint in an environment of several agents continuously receiving data according to arbitrary unknown agent-specific distributions. In particular, we provide a method based on hypothesis testing coupled with differential privacy and data variance estimation. Two privacy mechanisms and two data variance estimation schemes are proposed, and we provide a theoretical convergence analysis of the proposed algorithm for any bounded unknown distributions on the agents' data, showing that collaboration provides faster convergence than a fully local approach where agents do not share data. Moreover, we provide analytical performance curves for the case with an oracle class estimator, i.e., the class structure of the agents, where agents receiving data from distributions with the same mean are considered to be in the same class, is known. The theoretical faster-than-local convergence guarantee is backed up by extensive numerical results showing that for a considered scenario the proposed approach indeed converges much faster than a fully local approach, and performs comparably to ideal performance where all data is public. This illustrates the benefit of private collaboration in an online setting.

Age Aware Scheduling for Differentially-Private Federated Learning

This paper explores differentially-private federated learning (FL) across time-varying databases, delving into a nuanced three-way tradeoff involving age, accuracy, and differential privacy (DP). Emphasizing the potential advantages of scheduling, we propose an optimization problem aimed at meeting DP requirements while minimizing the loss difference between the aggregated model and the model obtained without DP constraints. To harness the benefits of scheduling, we introduce an age-dependent upper bound on the loss, leading to the development of an age-aware scheduling design. Simulation results underscore the superior performance of our proposed scheme compared to FL with classic DP, which does not consider scheduling as a design factor. This research contributes insights into the interplay of age, accuracy, and DP in federated learning, with practical implications for scheduling strategies.

Improved Capacity Outer Bound for Private Quadratic Monomial Computation

In private computation, a user wishes to retrieve a function evaluation of messages stored on a set of databases without revealing the function's identity to the databases. Obead \emph{et al.} introduced a capacity outer bound for private nonlinear computation, dependent on the order of the candidate functions. Focusing on private \emph{quadratic monomial} computation, we propose three methods for ordering candidate functions: a graph edge-coloring method, a graph-distance method, and an entropy-based greedy method. We confirm, via an exhaustive search, that all three methods yield an optimal ordering for $f < 6$ messages. For $6 \leq f \leq 12$ messages, we numerically evaluate the performance of the proposed methods compared with a directed random search. For almost all scenarios considered, the entropy-based greedy method gives the smallest gap to the best-found ordering.

Straggler-Resilient Differentially-Private Decentralized Learning

We consider the straggler problem in decentralized learning over a logical ring while preserving user data privacy. Especially, we extend the recently proposed framework of differential privacy (DP) amplification by decentralization by Cyffers and Bellet to include overall training latency--comprising both computation and communication latency. Analytical results on both the convergence speed and the DP level are derived for both a skipping scheme (which ignores the stragglers after a timeout) and a baseline scheme that waits for each node to finish before the training continues. A trade-off between overall training latency, accuracy, and privacy, parameterized by the timeout of the skipping scheme, is identified and empirically validated for logistic regression on a real-world dataset.

Generative Adversarial User Privacy in Lossy Single-Server Information Retrieval

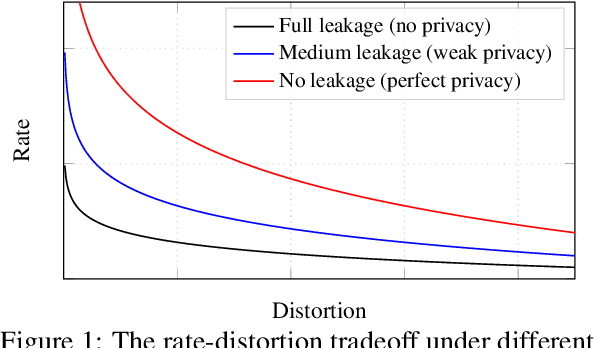
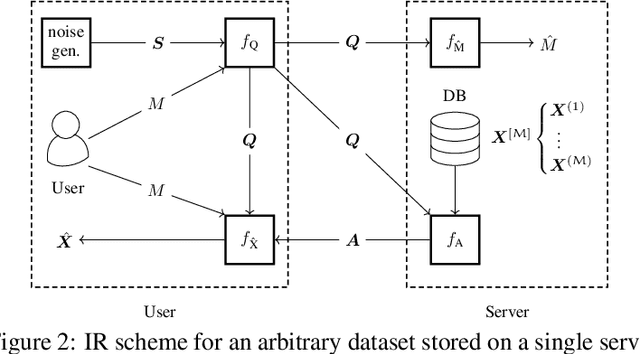
We consider the problem of information retrieval from a dataset of files stored on a single server under both a user distortion and a user privacy constraint. Specifically, a user requesting a file from the dataset should be able to reconstruct the requested file with a prescribed distortion, and in addition, the identity of the requested file should be kept private from the server with a prescribed privacy level. The proposed model can be seen as an extension of the well-known concept of private information retrieval by allowing for distortion in the retrieval process and relaxing the perfect privacy requirement. We initiate the study of the tradeoff between download rate, distortion, and user privacy leakage, and show that the optimal rate-distortion-leakage tradeoff is convex and that in the limit of large file sizes this allows for a concise information-theoretical formulation in terms of mutual information. Moreover, we propose a new data-driven framework by leveraging recent advancements in generative adversarial models which allows a user to learn efficient schemes in terms of download rate from the data itself. Learning the scheme is formulated as a constrained minimax game between a user which desires to keep the identity of the requested file private and an adversary that tries to infer which file the user is interested in under a distortion constraint. In general, guaranteeing a certain privacy level leads to a higher rate-distortion tradeoff curve, and hence a sacrifice in either download rate or distortion. We evaluate the performance of the scheme on a synthetic Gaussian dataset as well as on the MNIST and CIFAR-$10$ datasets. For the MNIST dataset, the data-driven approach significantly outperforms a proposed general achievable scheme combining source coding with the download of multiple files, while for CIFAR-$10$ the performances are comparable.