Arbitrariness Lies Beyond the Fairness-Accuracy Frontier

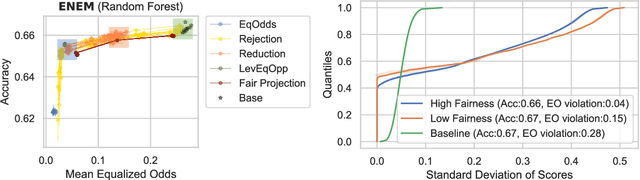
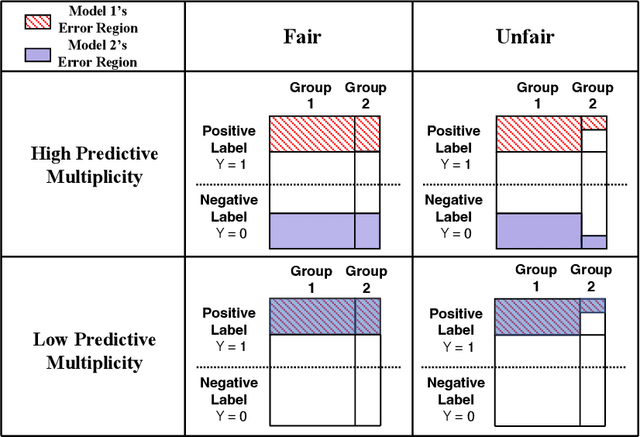
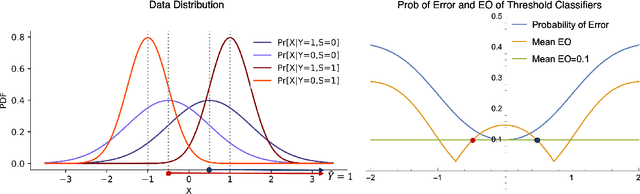
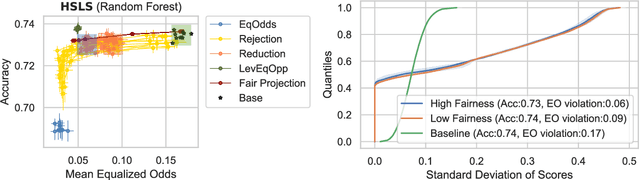
Machine learning tasks may admit multiple competing models that achieve similar performance yet produce conflicting outputs for individual samples -- a phenomenon known as predictive multiplicity. We demonstrate that fairness interventions in machine learning optimized solely for group fairness and accuracy can exacerbate predictive multiplicity. Consequently, state-of-the-art fairness interventions can mask high predictive multiplicity behind favorable group fairness and accuracy metrics. We argue that a third axis of ``arbitrariness'' should be considered when deploying models to aid decision-making in applications of individual-level impact. To address this challenge, we propose an ensemble algorithm applicable to any fairness intervention that provably ensures more consistent predictions.

The Saddle-Point Accountant for Differential Privacy

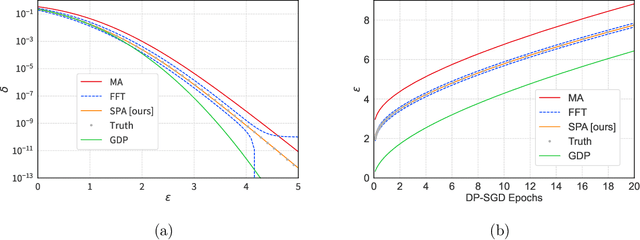
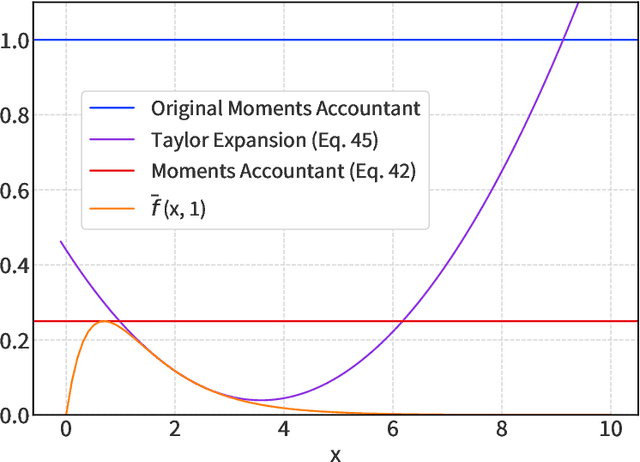
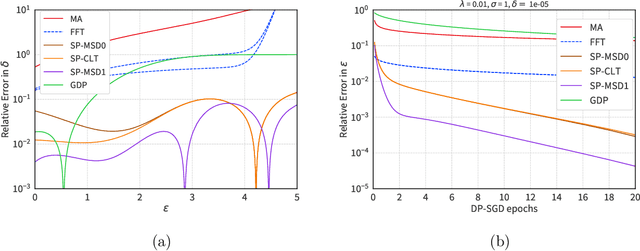
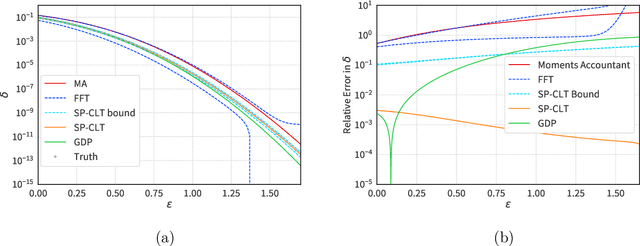
We introduce a new differential privacy (DP) accountant called the saddle-point accountant (SPA). SPA approximates privacy guarantees for the composition of DP mechanisms in an accurate and fast manner. Our approach is inspired by the saddle-point method -- a ubiquitous numerical technique in statistics. We prove rigorous performance guarantees by deriving upper and lower bounds for the approximation error offered by SPA. The crux of SPA is a combination of large-deviation methods with central limit theorems, which we derive via exponentially tilting the privacy loss random variables corresponding to the DP mechanisms. One key advantage of SPA is that it runs in constant time for the $n$-fold composition of a privacy mechanism. Numerical experiments demonstrate that SPA achieves comparable accuracy to state-of-the-art accounting methods with a faster runtime.

Cactus Mechanisms: Optimal Differential Privacy Mechanisms in the Large-Composition Regime

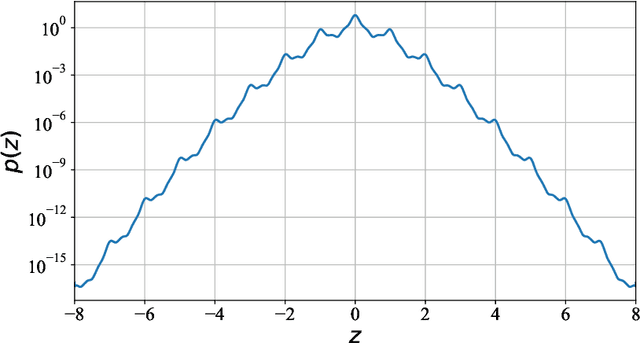
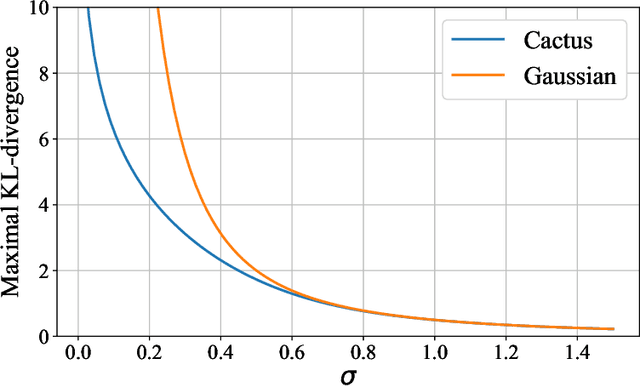
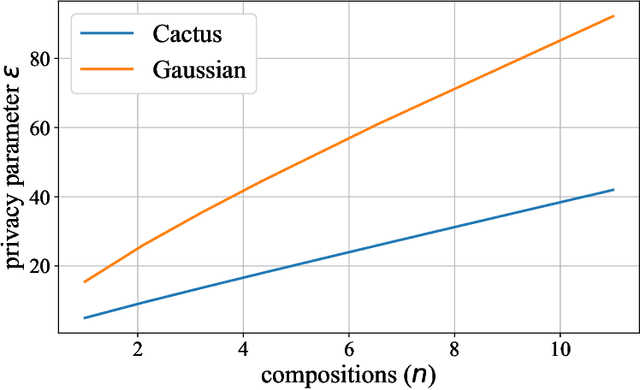
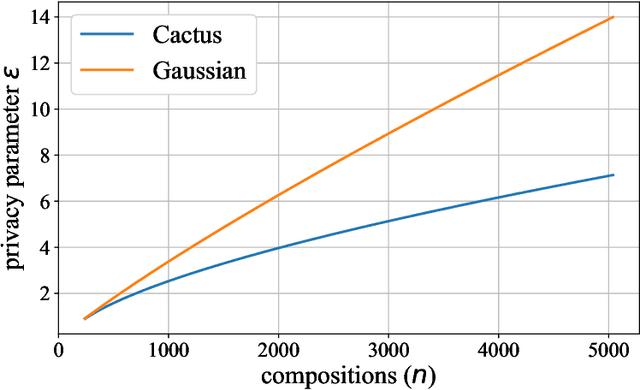
Most differential privacy mechanisms are applied (i.e., composed) numerous times on sensitive data. We study the design of optimal differential privacy mechanisms in the limit of a large number of compositions. As a consequence of the law of large numbers, in this regime the best privacy mechanism is the one that minimizes the Kullback-Leibler divergence between the conditional output distributions of the mechanism given two different inputs. We formulate an optimization problem to minimize this divergence subject to a cost constraint on the noise. We first prove that additive mechanisms are optimal. Since the optimization problem is infinite dimensional, it cannot be solved directly; nevertheless, we quantize the problem to derive near-optimal additive mechanisms that we call "cactus mechanisms" due to their shape. We show that our quantization approach can be arbitrarily close to an optimal mechanism. Surprisingly, for quadratic cost, the Gaussian mechanism is strictly sub-optimal compared to this cactus mechanism. Finally, we provide numerical results which indicate that cactus mechanism outperforms the Gaussian mechanism for a finite number of compositions.

Beyond Adult and COMPAS: Fairness in Multi-Class Prediction

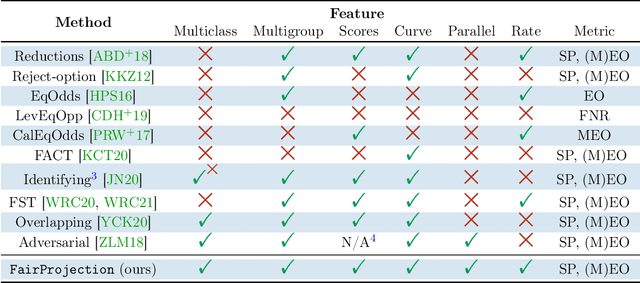
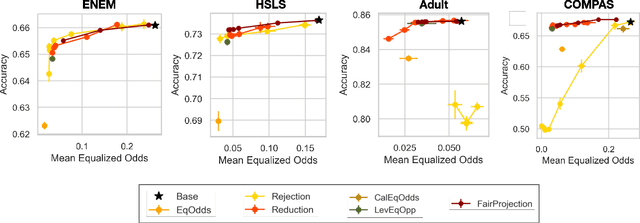
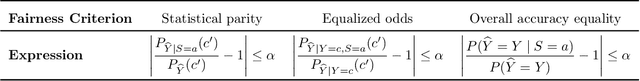
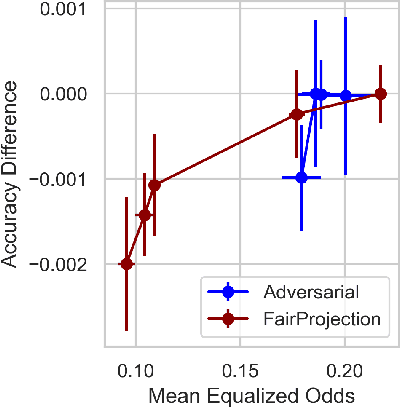
We consider the problem of producing fair probabilistic classifiers for multi-class classification tasks. We formulate this problem in terms of "projecting" a pre-trained (and potentially unfair) classifier onto the set of models that satisfy target group-fairness requirements. The new, projected model is given by post-processing the outputs of the pre-trained classifier by a multiplicative factor. We provide a parallelizable iterative algorithm for computing the projected classifier and derive both sample complexity and convergence guarantees. Comprehensive numerical comparisons with state-of-the-art benchmarks demonstrate that our approach maintains competitive performance in terms of accuracy-fairness trade-off curves, while achieving favorable runtime on large datasets. We also evaluate our method at scale on an open dataset with multiple classes, multiple intersectional protected groups, and over 1M samples.