Cactus Mechanisms: Optimal Differential Privacy Mechanisms in the Large-Composition Regime
Paper and Code
Jun 25, 2022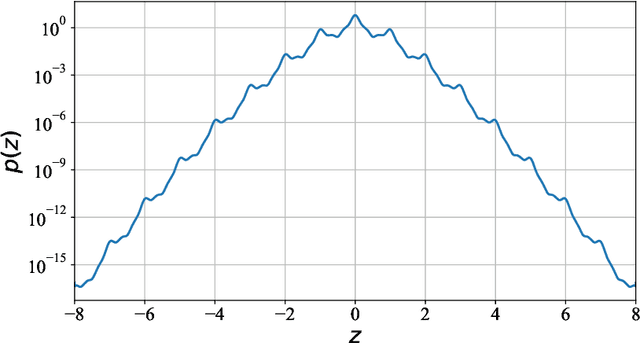
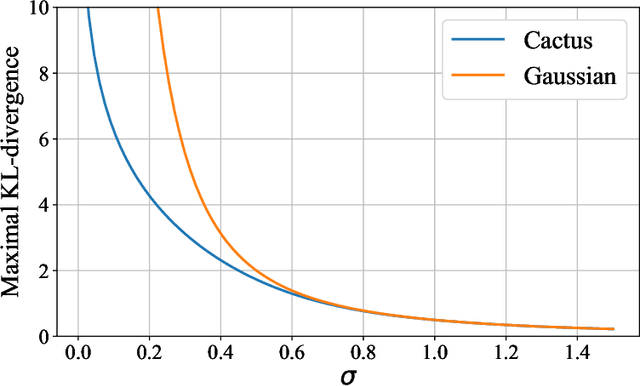
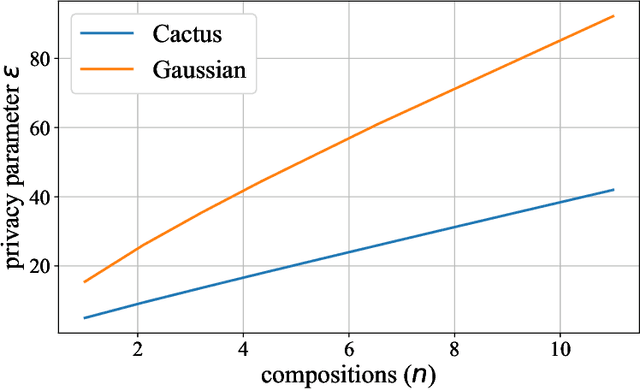
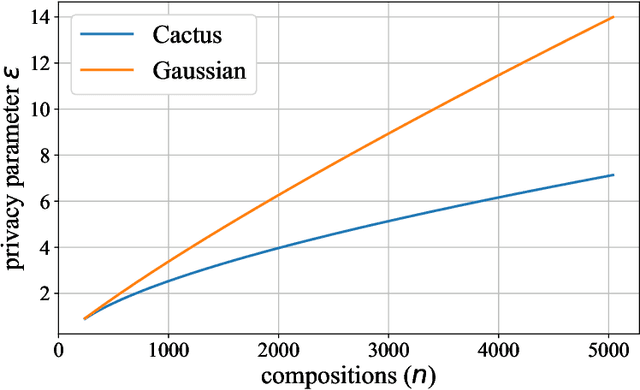
Most differential privacy mechanisms are applied (i.e., composed) numerous times on sensitive data. We study the design of optimal differential privacy mechanisms in the limit of a large number of compositions. As a consequence of the law of large numbers, in this regime the best privacy mechanism is the one that minimizes the Kullback-Leibler divergence between the conditional output distributions of the mechanism given two different inputs. We formulate an optimization problem to minimize this divergence subject to a cost constraint on the noise. We first prove that additive mechanisms are optimal. Since the optimization problem is infinite dimensional, it cannot be solved directly; nevertheless, we quantize the problem to derive near-optimal additive mechanisms that we call "cactus mechanisms" due to their shape. We show that our quantization approach can be arbitrarily close to an optimal mechanism. Surprisingly, for quadratic cost, the Gaussian mechanism is strictly sub-optimal compared to this cactus mechanism. Finally, we provide numerical results which indicate that cactus mechanism outperforms the Gaussian mechanism for a finite number of compositions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge