Certifiable Boolean Reasoning Is Universal

The proliferation of agentic systems has thrust the reasoning capabilities of AI into the forefront of contemporary machine learning. While it is known that there \emph{exist} neural networks which can reason through any Boolean task $f:\{0,1\}^B\to\{0,1\}$, in the sense that they emulate Boolean circuits with fan-in $2$ and fan-out $1$ gates, trained models have been repeatedly demonstrated to fall short of these theoretical ideals. This raises the question: \textit{Can one exhibit a deep learning model which \textbf{certifiably} always reasons and can \textbf{universally} reason through any Boolean task?} Moreover, such a model should ideally require few parameters to solve simple Boolean tasks. We answer this question affirmatively by exhibiting a deep learning architecture which parameterizes distributions over Boolean circuits with the guarantee that, for every parameter configuration, a sample is almost surely a valid Boolean circuit (and hence admits an intrinsic circuit-level certificate). We then prove a universality theorem: for any Boolean $f:\{0,1\}^B\to\{0,1\}$, there exists a parameter configuration under which the sampled circuit computes $f$ with arbitrarily high probability. When $f$ is an $\mathcal{O}(\log B)$-junta, the required number of parameters scales linearly with the input dimension $B$. Empirically, on a controlled truth-table completion benchmark aligned with our setting, the proposed architecture trains reliably and achieves high exact-match accuracy while preserving the predicted structure: every internal unit is Boolean-valued on $\{0,1\}^B$. Matched MLP baselines reach comparable accuracy, but only about $10\%$ of hidden units admit a Boolean representation; i.e.\ are two-valued over the Boolean cube.

A Closer Look at Personalized Fine-Tuning in Heterogeneous Federated Learning

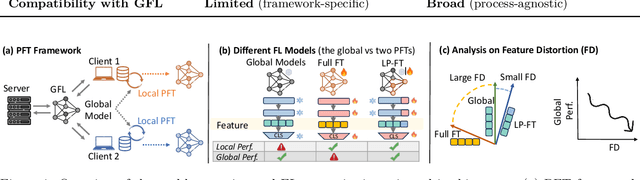
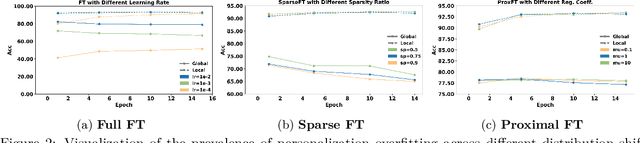
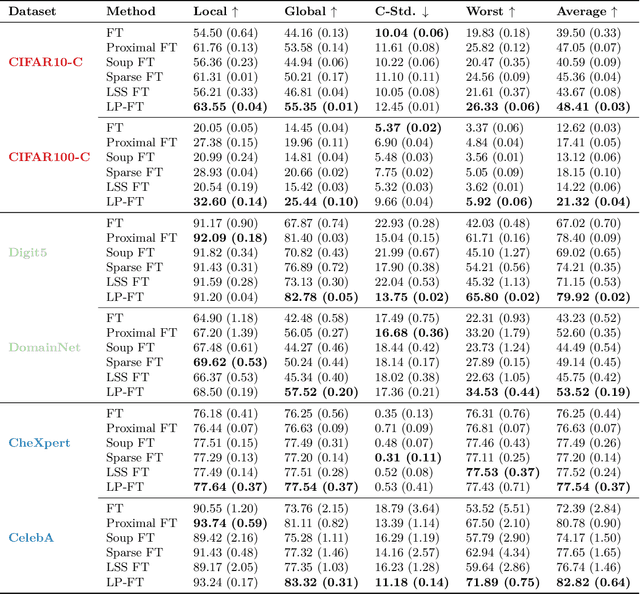
Federated Learning (FL) enables decentralized, privacy-preserving model training but struggles to balance global generalization and local personalization due to non-identical data distributions across clients. Personalized Fine-Tuning (PFT), a popular post-hoc solution, fine-tunes the final global model locally but often overfits to skewed client distributions or fails under domain shifts. We propose adapting Linear Probing followed by full Fine-Tuning (LP-FT), a principled centralized strategy for alleviating feature distortion (Kumar et al., 2022), to the FL setting. Through systematic evaluation across seven datasets and six PFT variants, we demonstrate LP-FT's superiority in balancing personalization and generalization. Our analysis uncovers federated feature distortion, a phenomenon where local fine-tuning destabilizes globally learned features, and theoretically characterizes how LP-FT mitigates this via phased parameter updates. We further establish conditions (e.g., partial feature overlap, covariate-concept shift) under which LP-FT outperforms standard fine-tuning, offering actionable guidelines for deploying robust personalization in FL.

Locally Optimal Private Sampling: Beyond the Global Minimax

We study the problem of sampling from a distribution under local differential privacy (LDP). Given a private distribution $P \in \mathcal{P}$, the goal is to generate a single sample from a distribution that remains close to $P$ in $f$-divergence while satisfying the constraints of LDP. This task captures the fundamental challenge of producing realistic-looking data under strong privacy guarantees. While prior work by Park et al. (NeurIPS'24) focuses on global minimax-optimality across a class of distributions, we take a local perspective. Specifically, we examine the minimax risk in a neighborhood around a fixed distribution $P_0$, and characterize its exact value, which depends on both $P_0$ and the privacy level. Our main result shows that the local minimax risk is determined by the global minimax risk when the distribution class $\mathcal{P}$ is restricted to a neighborhood around $P_0$. To establish this, we (1) extend previous work from pure LDP to the more general functional LDP framework, and (2) prove that the globally optimal functional LDP sampler yields the optimal local sampler when constrained to distributions near $P_0$. Building on this, we also derive a simple closed-form expression for the locally minimax-optimal samplers which does not depend on the choice of $f$-divergence. We further argue that this local framework naturally models private sampling with public data, where the public data distribution is represented by $P_0$. In this setting, we empirically compare our locally optimal sampler to existing global methods, and demonstrate that it consistently outperforms global minimax samplers.

Differentially Private Fair Binary Classifications

In this work, we investigate binary classification under the constraints of both differential privacy and fairness. We first propose an algorithm based on the decoupling technique for learning a classifier with only fairness guarantee. This algorithm takes in classifiers trained on different demographic groups and generates a single classifier satisfying statistical parity. We then refine this algorithm to incorporate differential privacy. The performance of the final algorithm is rigorously examined in terms of privacy, fairness, and utility guarantees. Empirical evaluations conducted on the Adult and Credit Card datasets illustrate that our algorithm outperforms the state-of-the-art in terms of fairness guarantees, while maintaining the same level of privacy and utility.