The Rate-Distortion-Perception Trade-off: The Role of Private Randomness

In image compression, with recent advances in generative modeling, the existence of a trade-off between the rate and the perceptual quality (realism) has been brought to light, where the realism is measured by the closeness of the output distribution to the source. It has been shown that randomized codes can be strictly better under a number of formulations. In particular, the role of common randomness has been well studied. We elucidate the role of private randomness in the compression of a memoryless source $X^n=(X_1,...,X_n)$ under two kinds of realism constraints. The near-perfect realism constraint requires the joint distribution of output symbols $(Y_1,...,Y_n)$ to be arbitrarily close the distribution of the source in total variation distance (TVD). The per-symbol near-perfect realism constraint requires that the TVD between the distribution of output symbol $Y_t$ and the source distribution be arbitrarily small, uniformly in the index $t.$ We characterize the corresponding asymptotic rate-distortion trade-off and show that encoder private randomness is not useful if the compression rate is lower than the entropy of the source, however limited the resources in terms of common randomness and decoder private randomness may be.

Wasserstein Distortion: Unifying Fidelity and Realism

We introduce a distortion measure for images, Wasserstein distortion, that simultaneously generalizes pixel-level fidelity on the one hand and realism on the other. We show how Wasserstein distortion reduces mathematically to a pure fidelity constraint or a pure realism constraint under different parameter choices. Pairs of images that are close under Wasserstein distortion illustrate its utility. In particular, we generate random textures that have high fidelity to a reference texture in one location of the image and smoothly transition to an independent realization of the texture as one moves away from this point. Connections between Wasserstein distortion and models of the human visual system are noted.

Do Neural Networks Compress Manifolds Optimally?

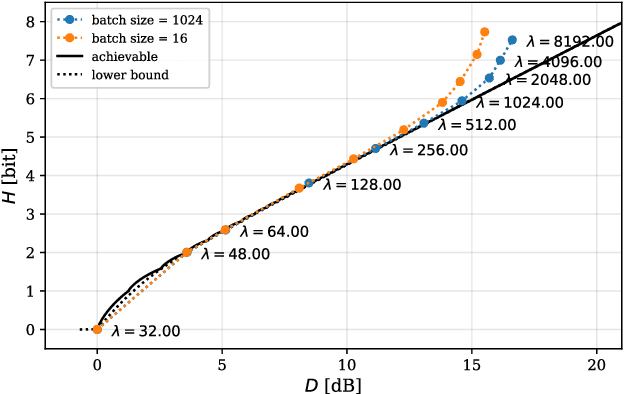
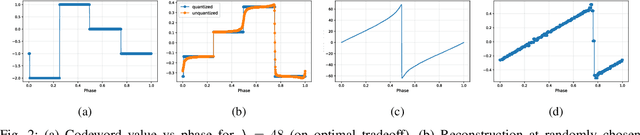
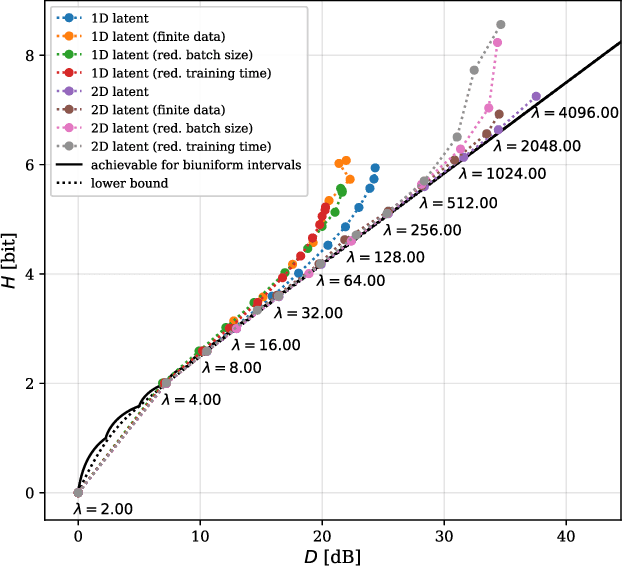
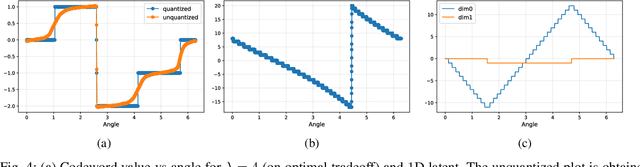
Artificial Neural-Network-based (ANN-based) lossy compressors have recently obtained striking results on several sources. Their success may be ascribed to an ability to identify the structure of low-dimensional manifolds in high-dimensional ambient spaces. Indeed, prior work has shown that ANN-based compressors can achieve the optimal entropy-distortion curve for some such sources. In contrast, we determine the optimal entropy-distortion tradeoffs for two low-dimensional manifolds with circular structure and show that state-of-the-art ANN-based compressors fail to optimally compress the sources, especially at high rates.

On One-Bit Quantization

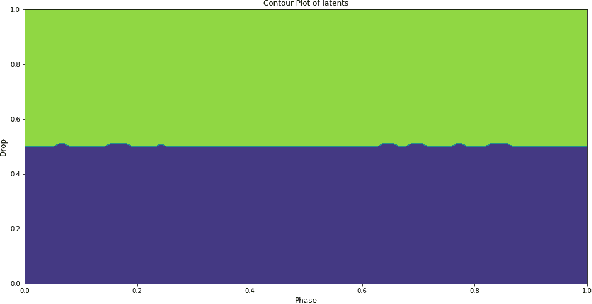
We consider the one-bit quantizer that minimizes the mean squared error for a source living in a real Hilbert space. The optimal quantizer is a projection followed by a thresholding operation, and we provide methods for identifying the optimal direction along which to project. As an application of our methods, we characterize the optimal one-bit quantizer for a continuous-time random process that exhibits low-dimensional structure. We numerically show that this optimal quantizer is found by a neural-network-based compressor trained via stochastic gradient descent.

The Rate-Distortion-Perception Tradeoff: The Role of Common Randomness

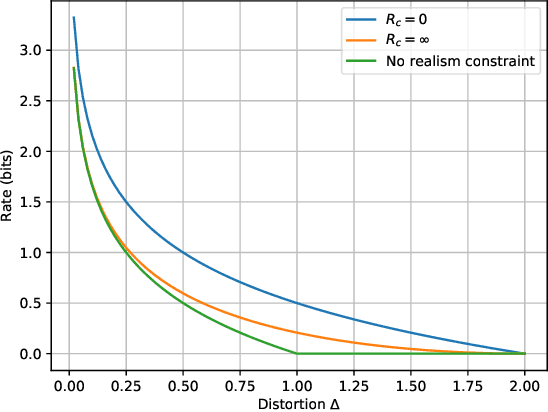
A rate-distortion-perception (RDP) tradeoff has recently been proposed by Blau and Michaeli and also Matsumoto. Focusing on the case of perfect realism, which coincides with the problem of distribution-preserving lossy compression studied by Li et al., a coding theorem for the RDP tradeoff that allows for a specified amount of common randomness between the encoder and decoder is provided. The existing RDP tradeoff is recovered by allowing for the amount of common randomness to be infinite. The quadratic Gaussian case is examined in detail.

Principal Bit Analysis: Autoencoding with Schur-Concave Loss

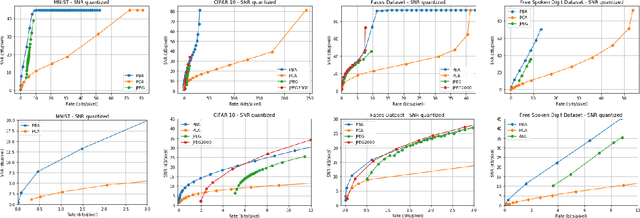
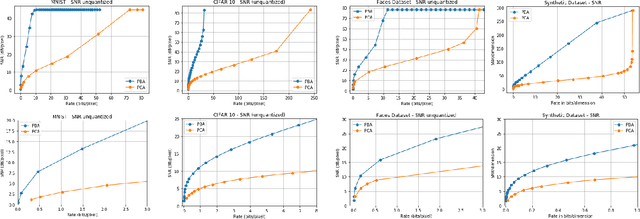
We consider a linear autoencoder in which the latent variables are quantized, or corrupted by noise, and the constraint is Schur-concave in the set of latent variances. Although finding the optimal encoder/decoder pair for this setup is a nonconvex optimization problem, we show that decomposing the source into its principal components is optimal. If the constraint is strictly Schur-concave and the empirical covariance matrix has only simple eigenvalues, then any optimal encoder/decoder must decompose the source in this way. As one application, we consider a strictly Schur-concave constraint that estimates the number of bits needed to represent the latent variables under fixed-rate encoding, a setup that we call \emph{Principal Bit Analysis (PBA)}. This yields a practical, general-purpose, fixed-rate compressor that outperforms existing algorithms. As a second application, we show that a prototypical autoencoder-based variable-rate compressor is guaranteed to decompose the source into its principal components.

A coding theorem for the rate-distortion-perception function

The rate-distortion-perception function (RDPF; Blau and Michaeli, 2019) has emerged as a useful tool for thinking about realism and distortion of reconstructions in lossy compression. Unlike the rate-distortion function, however, it is unknown whether encoders and decoders exist that achieve the rate suggested by the RDPF. Building on results by Li and El Gamal (2018), we show that the RDPF can indeed be achieved using stochastic, variable-length codes. For this class of codes, we also prove that the RDPF lower-bounds the achievable rate