Do Neural Networks Compress Manifolds Optimally?

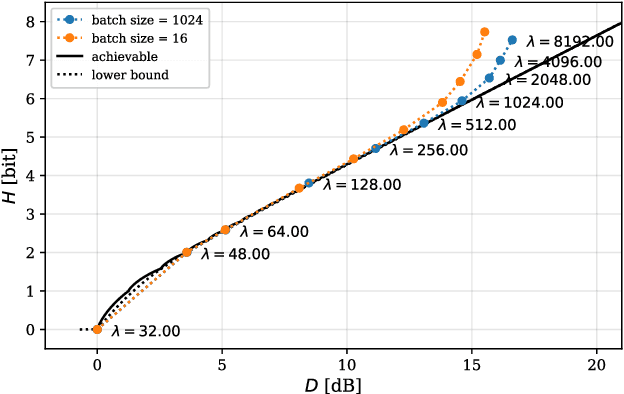
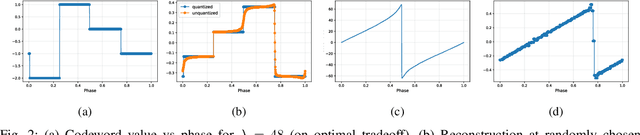
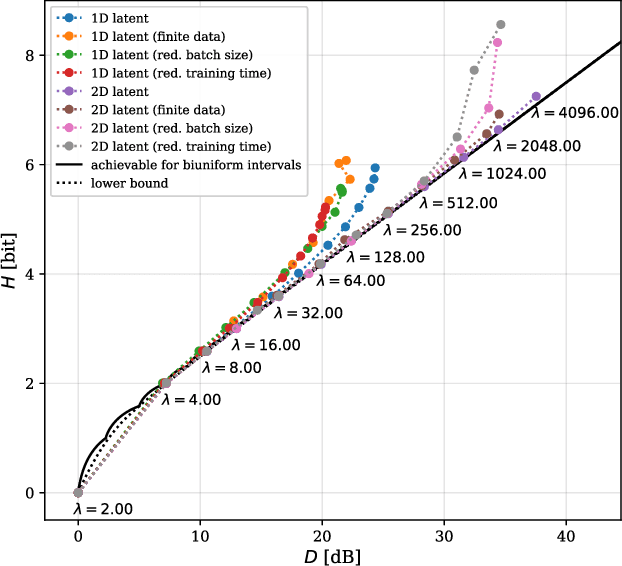
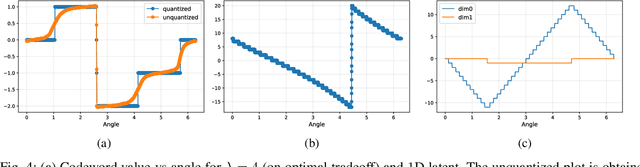
Artificial Neural-Network-based (ANN-based) lossy compressors have recently obtained striking results on several sources. Their success may be ascribed to an ability to identify the structure of low-dimensional manifolds in high-dimensional ambient spaces. Indeed, prior work has shown that ANN-based compressors can achieve the optimal entropy-distortion curve for some such sources. In contrast, we determine the optimal entropy-distortion tradeoffs for two low-dimensional manifolds with circular structure and show that state-of-the-art ANN-based compressors fail to optimally compress the sources, especially at high rates.

On One-Bit Quantization

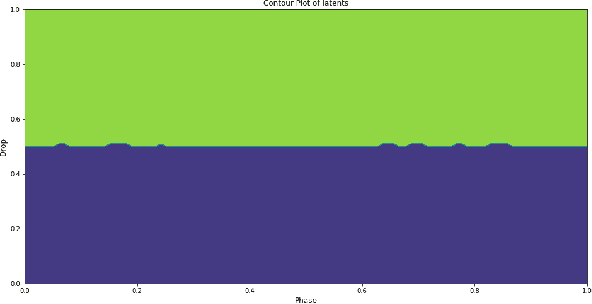
We consider the one-bit quantizer that minimizes the mean squared error for a source living in a real Hilbert space. The optimal quantizer is a projection followed by a thresholding operation, and we provide methods for identifying the optimal direction along which to project. As an application of our methods, we characterize the optimal one-bit quantizer for a continuous-time random process that exhibits low-dimensional structure. We numerically show that this optimal quantizer is found by a neural-network-based compressor trained via stochastic gradient descent.

Principal Bit Analysis: Autoencoding with Schur-Concave Loss

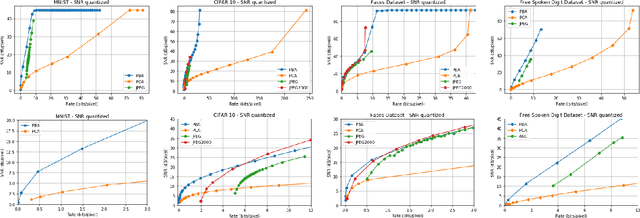
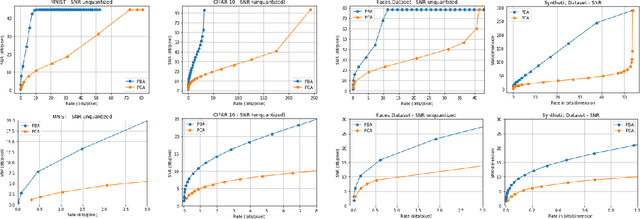
We consider a linear autoencoder in which the latent variables are quantized, or corrupted by noise, and the constraint is Schur-concave in the set of latent variances. Although finding the optimal encoder/decoder pair for this setup is a nonconvex optimization problem, we show that decomposing the source into its principal components is optimal. If the constraint is strictly Schur-concave and the empirical covariance matrix has only simple eigenvalues, then any optimal encoder/decoder must decompose the source in this way. As one application, we consider a strictly Schur-concave constraint that estimates the number of bits needed to represent the latent variables under fixed-rate encoding, a setup that we call \emph{Principal Bit Analysis (PBA)}. This yields a practical, general-purpose, fixed-rate compressor that outperforms existing algorithms. As a second application, we show that a prototypical autoencoder-based variable-rate compressor is guaranteed to decompose the source into its principal components.

Estimating Entropy of Distributions in Constant Space

We consider the task of estimating the entropy of $k$-ary distributions from samples in the streaming model, where space is limited. Our main contribution is an algorithm that requires $O\left(\frac{k \log (1/\varepsilon)^2}{\varepsilon^3}\right)$ samples and a constant $O(1)$ memory words of space and outputs a $\pm\varepsilon$ estimate of $H(p)$. Without space limitations, the sample complexity has been established as $S(k,\varepsilon)=\Theta\left(\frac k{\varepsilon\log k}+\frac{\log^2 k}{\varepsilon^2}\right)$, which is sub-linear in the domain size $k$, and the current algorithms that achieve optimal sample complexity also require nearly-linear space in $k$. Our algorithm partitions $[0,1]$ into intervals and estimates the entropy contribution of probability values in each interval. The intervals are designed to trade off the bias and variance of these estimates.