The Rate-Distortion-Perception Tradeoff: The Role of Common Randomness
Paper and Code
Feb 08, 2022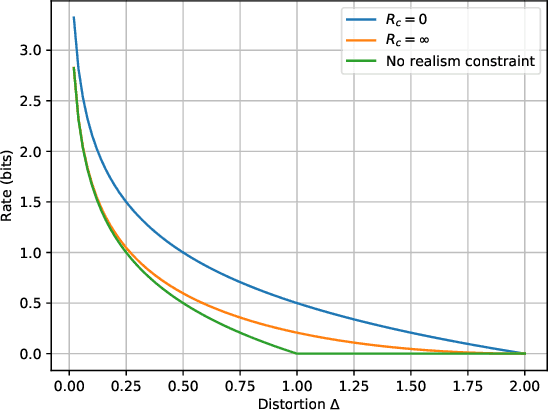
A rate-distortion-perception (RDP) tradeoff has recently been proposed by Blau and Michaeli and also Matsumoto. Focusing on the case of perfect realism, which coincides with the problem of distribution-preserving lossy compression studied by Li et al., a coding theorem for the RDP tradeoff that allows for a specified amount of common randomness between the encoder and decoder is provided. The existing RDP tradeoff is recovered by allowing for the amount of common randomness to be infinite. The quadratic Gaussian case is examined in detail.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge