General lower bounds for interactive high-dimensional estimation under information constraints

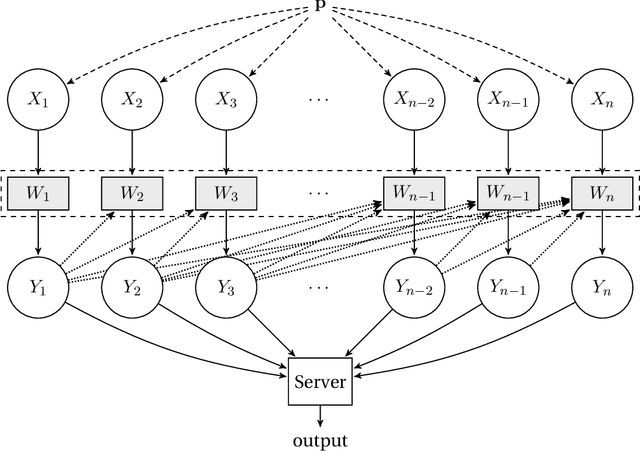
We consider the task of distributed parameter estimation using sequentially interactive protocols subject to local information constraints such as bandwidth limitations, local differential privacy, and restricted measurements. We provide a general framework enabling us to derive a variety of (tight) minimax lower bounds under different parametric families of distributions, both continuous and discrete, under any $\ell_p$ loss. Our lower bound framework is versatile, and yields "plug-and-play" bounds that are widely applicable to a large range of estimation problems. In particular, our approach recovers bounds obtained using data processing inequalities and Cram\'er-Rao bounds, two other alternative approaches for proving lower bounds in our setting of interest. Further, for the families considered, we complement our lower bounds with matching upper bounds.