Interactive Inference under Information Constraints

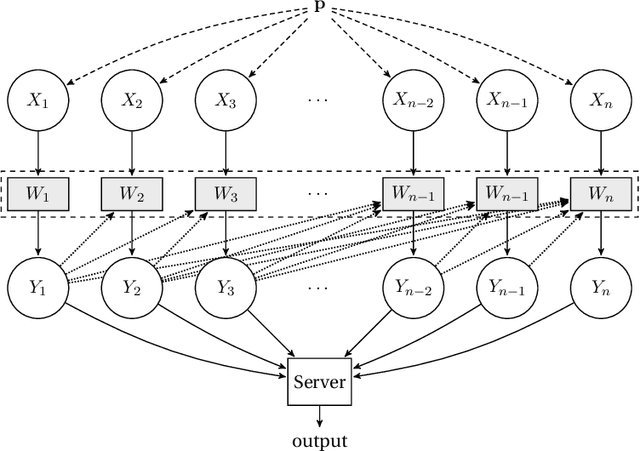
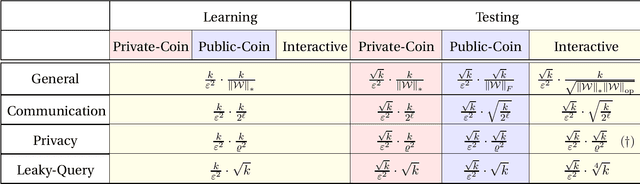
We consider distributed inference using sequentially interactive protocols. We obtain lower bounds on the minimax sample complexity of interactive protocols under local information constraints, a broad family of resource constraints which captures communication constraints, local differential privacy, and noisy binary queries as special cases. We focus on the inference tasks of learning (density estimation) and identity testing (goodness-of-fit) for discrete distributions under total variation distance, and establish general lower bounds that take into account the local constraints modeled as a channel family. Our main technical contribution is an approach to handle the correlation that builds due to interactivity and quantifies how effectively one can exploit this correlation in spite of the local constraints. Using this, we fill gaps in some prior works and characterize the optimal sample complexity of learning and testing discrete distributions under total variation distance, for both communication and local differential privacy constraints. Prior to our work, this was known only for the problem of testing under local privacy constraints (Amin, Joseph, and Mao (2020); Berrett and Butucea (2020)). Our results show that interactivity does not help for learning or testing under these two constraints. Finally, we provide the first instance of a natural family of "leaky query" local constraints under which interactive protocols strictly outperform the noninteractive ones for distribution testing.