Generalizing Bottleneck Problems
Paper and Code
May 10, 2018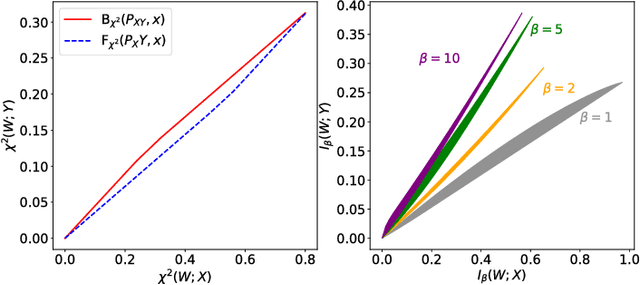
Given a pair of random variables $(X,Y)\sim P_{XY}$ and two convex functions $f_1$ and $f_2$, we introduce two bottleneck functionals as the lower and upper boundaries of the two-dimensional convex set that consists of the pairs $\left(I_{f_1}(W; X), I_{f_2}(W; Y)\right)$, where $I_f$ denotes $f$-information and $W$ varies over the set of all discrete random variables satisfying the Markov condition $W \to X \to Y$. Applying Witsenhausen and Wyner's approach, we provide an algorithm for computing boundaries of this set for $f_1$, $f_2$, and discrete $P_{XY}$. In the binary symmetric case, we fully characterize the set when (i) $f_1(t)=f_2(t)=t\log t$, (ii) $f_1(t)=f_2(t)=t^2-1$, and (iii) $f_1$ and $f_2$ are both $\ell^\beta$ norm function for $\beta \geq 2$. We then argue that upper and lower boundaries in (i) correspond to Mrs. Gerber's Lemma and its inverse (which we call Mr. Gerber's Lemma), in (ii) correspond to estimation-theoretic variants of Information Bottleneck and Privacy Funnel, and in (iii) correspond to Arimoto Information Bottleneck and Privacy Funnel.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge