Measuring Re-identification Risk

Compact user representations (such as embeddings) form the backbone of personalization services. In this work, we present a new theoretical framework to measure re-identification risk in such user representations. Our framework, based on hypothesis testing, formally bounds the probability that an attacker may be able to obtain the identity of a user from their representation. As an application, we show how our framework is general enough to model important real-world applications such as the Chrome's Topics API for interest-based advertising. We complement our theoretical bounds by showing provably good attack algorithms for re-identification that we use to estimate the re-identification risk in the Topics API. We believe this work provides a rigorous and interpretable notion of re-identification risk and a framework to measure it that can be used to inform real-world applications.

Smooth Anonymity for Sparse Binary Matrices

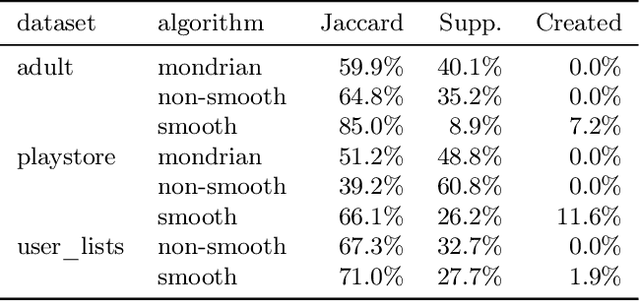
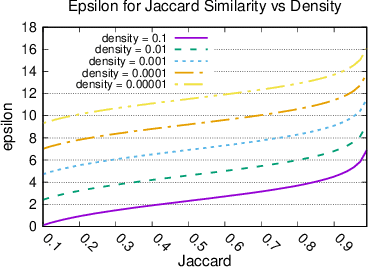
When working with user data providing well-defined privacy guarantees is paramount. In this work we aim to manipulate and share an entire sparse dataset with a third party privately. In fact, differential privacy has emerged as the gold standard of privacy, however, when it comes to sharing sparse datasets, as one of our main results, we prove that \emph{any} differentially private mechanism that maintains a reasonable similarity with the initial dataset is doomed to have a very weak privacy guarantee. Hence we need to opt for other privacy notions such as $k$-anonymity are better at preserving utility in this context. In this work we present a variation of $k$-anonymity, which we call smooth $k$-anonymity and design simple algorithms that efficiently provide smooth $k$-anonymity. We further perform an empirical evaluation to back our theoretical guarantees, and show that our algorithm improves the performance in downstream machine learning tasks on anonymized data.

Non-parametric Revenue Optimization for Generalized Second Price Auctions

We present an extensive analysis of the key problem of learning optimal reserve prices for generalized second price auctions. We describe two algorithms for this task: one based on density estimation, and a novel algorithm benefiting from solid theoretical guarantees and with a very favorable running-time complexity of $O(n S \log (n S))$, where $n$ is the sample size and $S$ the number of slots. Our theoretical guarantees are more favorable than those previously presented in the literature. Additionally, we show that even if bidders do not play at an equilibrium, our second algorithm is still well defined and minimizes a quantity of interest. To our knowledge, this is the first attempt to apply learning algorithms to the problem of reserve price optimization in GSP auctions. Finally, we present the first convergence analysis of empirical equilibrium bidding functions to the unique symmetric Bayesian-Nash equilibrium of a GSP.

New Analysis and Algorithm for Learning with Drifting Distributions

We present a new analysis of the problem of learning with drifting distributions in the batch setting using the notion of discrepancy. We prove learning bounds based on the Rademacher complexity of the hypothesis set and the discrepancy of distributions both for a drifting PAC scenario and a tracking scenario. Our bounds are always tighter and in some cases substantially improve upon previous ones based on the $L_1$ distance. We also present a generalization of the standard on-line to batch conversion to the drifting scenario in terms of the discrepancy and arbitrary convex combinations of hypotheses. We introduce a new algorithm exploiting these learning guarantees, which we show can be formulated as a simple QP. Finally, we report the results of preliminary experiments demonstrating the benefits of this algorithm.