Sample-Optimal Private Regression in Polynomial Time

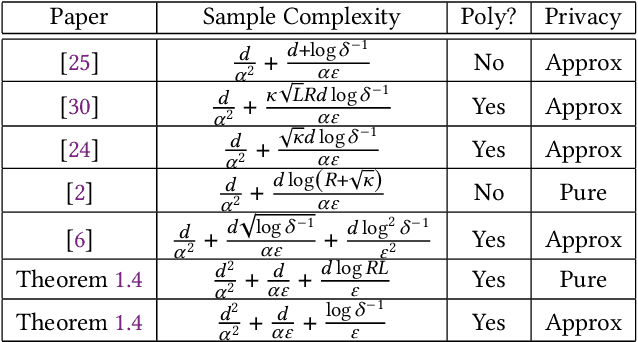
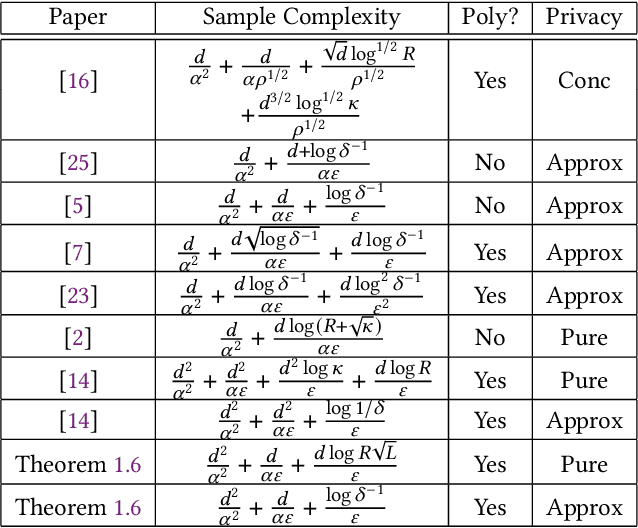
We consider the task of privately obtaining prediction error guarantees in ordinary least-squares regression problems with Gaussian covariates (with unknown covariance structure). We provide the first sample-optimal polynomial time algorithm for this task under both pure and approximate differential privacy. We show that any improvement to the sample complexity of our algorithm would violate either statistical-query or information-theoretic lower bounds. Additionally, our algorithm is robust to a small fraction of arbitrary outliers and achieves optimal error rates as a function of the fraction of outliers. In contrast, all prior efficient algorithms either incurred sample complexities with sub-optimal dimension dependence, scaling with the condition number of the covariates, or obtained a polynomially worse dependence on the privacy parameters. Our technical contributions are two-fold: first, we leverage resilience guarantees of Gaussians within the sum-of-squares framework. As a consequence, we obtain efficient sum-of-squares algorithms for regression with optimal robustness rates and sample complexity. Second, we generalize the recent robustness-to-privacy framework [HKMN23, (arXiv:2212.05015)] to account for the geometry induced by the covariance of the input samples. This framework crucially relies on the robust estimators to be sum-of-squares algorithms, and combining the two steps yields a sample-optimal private regression algorithm. We believe our techniques are of independent interest, and we demonstrate this by obtaining an efficient algorithm for covariance-aware mean estimation, with an optimal dependence on the privacy parameters.

Dimension Reduction via Sum-of-Squares and Improved Clustering Algorithms for Non-Spherical Mixtures

We develop a new approach for clustering non-spherical (i.e., arbitrary component covariances) Gaussian mixture models via a subroutine, based on the sum-of-squares method, that finds a low-dimensional separation-preserving projection of the input data. Our method gives a non-spherical analog of the classical dimension reduction, based on singular value decomposition, that forms a key component of the celebrated spherical clustering algorithm of Vempala and Wang [VW04] (in addition to several other applications). As applications, we obtain an algorithm to (1) cluster an arbitrary total-variation separated mixture of $k$ centered (i.e., zero-mean) Gaussians with $n\geq \operatorname{poly}(d) f(w_{\min}^{-1})$ samples and $\operatorname{poly}(n)$ time, and (2) cluster an arbitrary total-variation separated mixture of $k$ Gaussians with identical but arbitrary unknown covariance with $n \geq d^{O(\log w_{\min}^{-1})} f(w_{\min}^{-1})$ samples and $n^{O(\log w_{\min}^{-1})}$ time. Here, $w_{\min}$ is the minimum mixing weight of the input mixture, and $f$ does not depend on the dimension $d$. Our algorithms naturally extend to tolerating a dimension-independent fraction of arbitrary outliers. Before this work, the techniques in the state-of-the-art non-spherical clustering algorithms needed $d^{O(k)} f(w_{\min}^{-1})$ time and samples for clustering such mixtures. Our results may come as a surprise in the context of the $d^{\Omega(k)}$ statistical query lower bound [DKS17] for clustering non-spherical Gaussian mixtures. While this result is usually thought to rule out $d^{o(k)}$ cost algorithms for the problem, our results show that the lower bounds can in fact be circumvented for a remarkably general class of Gaussian mixtures.