Efficiently Learning Markov Random Fields from Dynamics

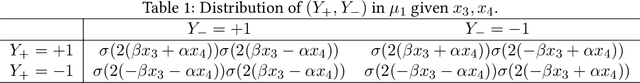
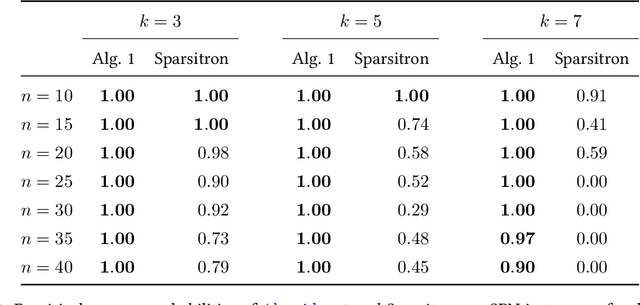
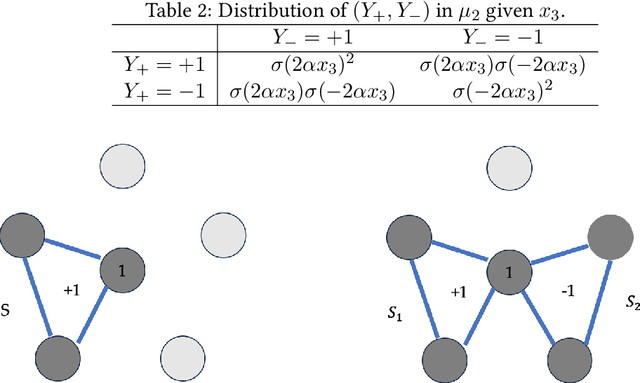
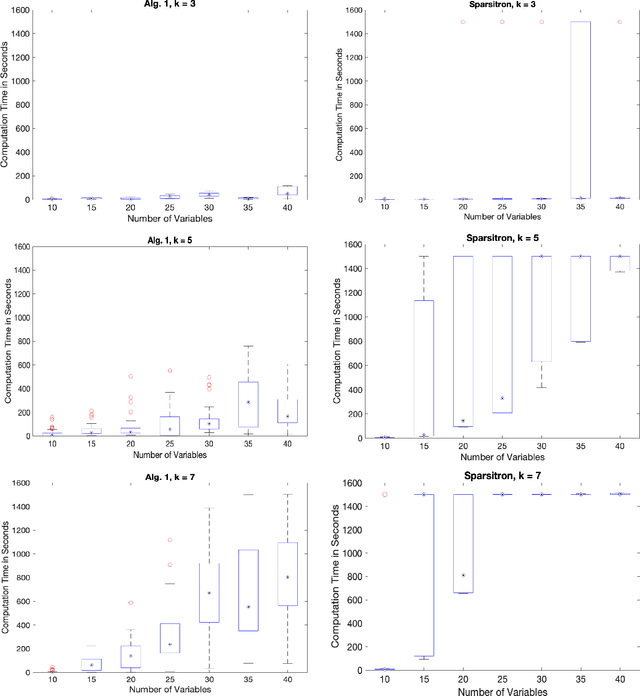
An important task in high-dimensional statistics is learning the parameters or dependency structure of an undirected graphical model, or Markov random field (MRF). Much of the prior work on this problem assumes access to i.i.d. samples from the MRF distribution and state-of-the-art algorithms succeed using $n^{\Theta(k)}$ runtime, where $n$ is the dimension and $k$ is the order of the interactions. However, well-known reductions from the sparse parity with noise problem imply that given i.i.d. samples from a sparse, order-$k$ MRF, any learning algorithm likely requires $n^{\Omega(k)}$ time, impeding the potential for significant computational improvements. In this work, we demonstrate that these fundamental barriers for learning MRFs can surprisingly be completely circumvented when learning from natural, dynamical samples. We show that in bounded-degree MRFs, the dependency structure and parameters can be recovered using a trajectory of Glauber dynamics of length $O(n \log n)$ with runtime $O(n^2 \log n)$. The implicit constants depend only on the degree and non-degeneracy parameters of the model, but not the dimension $n$. In particular, learning MRFs from dynamics is $\textit{provably computationally easier}$ than learning from i.i.d. samples under standard hardness assumptions.

Sample-Efficient Linear Regression with Self-Selection Bias

We consider the problem of linear regression with self-selection bias in the unknown-index setting, as introduced in recent work by Cherapanamjeri, Daskalakis, Ilyas, and Zampetakis [STOC 2023]. In this model, one observes $m$ i.i.d. samples $(\mathbf{x}_{\ell},z_{\ell})_{\ell=1}^m$ where $z_{\ell}=\max_{i\in [k]}\{\mathbf{x}_{\ell}^T\mathbf{w}_i+\eta_{i,\ell}\}$, but the maximizing index $i_{\ell}$ is unobserved. Here, the $\mathbf{x}_{\ell}$ are assumed to be $\mathcal{N}(0,I_n)$ and the noise distribution $\mathbf{\eta}_{\ell}\sim \mathcal{D}$ is centered and independent of $\mathbf{x}_{\ell}$. We provide a novel and near optimally sample-efficient (in terms of $k$) algorithm to recover $\mathbf{w}_1,\ldots,\mathbf{w}_k\in \mathbb{R}^n$ up to additive $\ell_2$-error $\varepsilon$ with polynomial sample complexity $\tilde{O}(n)\cdot \mathsf{poly}(k,1/\varepsilon)$ and significantly improved time complexity $\mathsf{poly}(n,k,1/\varepsilon)+O(\log(k)/\varepsilon)^{O(k)}$. When $k=O(1)$, our algorithm runs in $\mathsf{poly}(n,1/\varepsilon)$ time, generalizing the polynomial guarantee of an explicit moment matching algorithm of Cherapanamjeri, et al. for $k=2$ and when it is known that $\mathcal{D}=\mathcal{N}(0,I_k)$. Our algorithm succeeds under significantly relaxed noise assumptions, and therefore also succeeds in the related setting of max-linear regression where the added noise is taken outside the maximum. For this problem, our algorithm is efficient in a much larger range of $k$ than the state-of-the-art due to Ghosh, Pananjady, Guntuboyina, and Ramchandran [IEEE Trans. Inf. Theory 2022] for not too small $\varepsilon$, and leads to improved algorithms for any $\varepsilon$ by providing a warm start for existing local convergence methods.

A Unified Approach to Learning Ising Models: Beyond Independence and Bounded Width

We revisit the problem of efficiently learning the underlying parameters of Ising models from data. Current algorithmic approaches achieve essentially optimal sample complexity when given i.i.d. samples from the stationary measure and the underlying model satisfies "width" bounds on the total $\ell_1$ interaction involving each node. We show that a simple existing approach based on node-wise logistic regression provably succeeds at recovering the underlying model in several new settings where these assumptions are violated: (1) Given dynamically generated data from a wide variety of local Markov chains, like block or round-robin dynamics, logistic regression recovers the parameters with optimal sample complexity up to $\log\log n$ factors. This generalizes the specialized algorithm of Bresler, Gamarnik, and Shah [IEEE Trans. Inf. Theory'18] for structure recovery in bounded degree graphs from Glauber dynamics. (2) For the Sherrington-Kirkpatrick model of spin glasses, given $\mathsf{poly}(n)$ independent samples, logistic regression recovers the parameters in most of the known high-temperature regime via a simple reduction to weaker structural properties of the measure. This improves on recent work of Anari, Jain, Koehler, Pham, and Vuong [ArXiv'23] which gives distribution learning at higher temperature. (3) As a simple byproduct of our techniques, logistic regression achieves an exponential improvement in learning from samples in the M-regime of data considered by Dutt, Lokhov, Vuffray, and Misra [ICML'21] as well as novel guarantees for learning from the adversarial Glauber dynamics of Chin, Moitra, Mossel, and Sandon [ArXiv'23]. Our approach thus significantly generalizes the elegant analysis of Wu, Sanghavi, and Dimakis [Neurips'19] without any algorithmic modification.

Stability and Learning in Strategic Queuing Systems

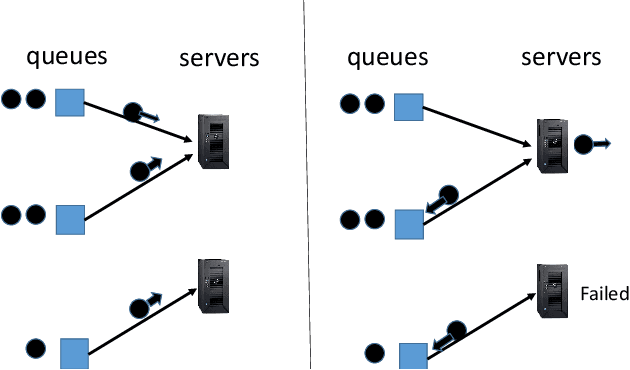
Bounding the price of anarchy, which quantifies the damage to social welfare due to selfish behavior of the participants, has been an important area of research. In this paper, we study this phenomenon in the context of a game modeling queuing systems: routers compete for servers, where packets that do not get service will be resent at future rounds, resulting in a system where the number of packets at each round depends on the success of the routers in the previous rounds. We model this as an (infinitely) repeated game, where the system holds a state (number of packets held by each queue) that arises from the results of the previous round. We assume that routers satisfy the no-regret condition, e.g. they use learning strategies to identify the server where their packets get the best service. Classical work on repeated games makes the strong assumption that the subsequent rounds of the repeated games are independent (beyond the influence on learning from past history). The carryover effect caused by packets remaining in this system makes learning in our context result in a highly dependent random process. We analyze this random process and find that if the capacity of the servers is high enough to allow a centralized and knowledgeable scheduler to get all packets served even with double the packet arrival rate, and queues use no-regret learning algorithms, then the expected number of packets in the queues will remain bounded throughout time, assuming older packets have priority. This paper is the first to study the effect of selfish learning in a queuing system, where the learners compete for resources, but rounds are not all independent: the number of packets to be routed at each round depends on the success of the routers in the previous rounds.