Learning in Strategic Queuing Systems with Small Buffers

Routers in networking use simple learning algorithms to find the best way to deliver packets to their desired destination. This simple, myopic and distributed decision system makes large queuing systems simple to operate, but at the same time, the system needs more capacity than would be required if all traffic were centrally coordinated. In a recent paper, Gaitonde and Tardos (EC 2020 and JACM 2023) initiate the study of such systems, modeling them as an infinitely repeated game in which routers compete for servers and the system maintains a state (number of packets held by each queue) resulting from outcomes of previous rounds. Queues get to send a packet at each step to one of the servers, and servers attempt to process only one of the arriving packets, modeling routers. However, their model assumes that servers have no buffers at all, so queues have to resend all packets that were not served successfully. They show that, even with hugely increased server capacity relative to what is needed in the centrally-coordinated case, ensuring that the system is stable requires using timestamps and priority for older packets. We consider a system with two important changes, which make the model more realistic: first we add a very small buffer to each server, allowing it to hold on to a single packet to be served later (even if it fails to serve it); and second, we do not require timestamps or priority for older packets. Our main result is to show that when queues are learning, a small constant factor increase in server capacity, compared to what would be needed if centrally coordinating, suffices to keep the system stable, even if servers select randomly among packets arriving simultaneously. This work contributes to the growing literature on the impact of selfish learning in systems with carryover effects between rounds: when outcomes in the present round affect the game in the future.

Learning in Markets with Heterogeneous Agents: Dynamics and Survival of Bayesian vs. No-Regret Learners

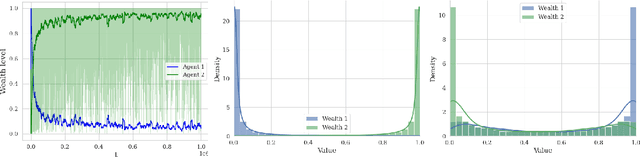
We analyze the performance of heterogeneous learning agents in asset markets with stochastic payoffs. Our agents aim to maximize the expected growth rate of their wealth but have different theories on how to learn this best. We focus on comparing Bayesian and no-regret learners in market dynamics. Bayesian learners with a prior over a finite set of models that assign positive prior probability to the correct model have posterior probabilities that converge exponentially to the correct model. Consequently, they survive even in the presence of agents who invest according to the correct model of the stochastic process. Bayesians with a continuum prior converge to the correct model at a rate of $O((\log T)/T)$. Online learning theory provides no-regret algorithms for maximizing the log of wealth in this setting, achieving a worst-case regret bound of $O(\log T)$ without assuming a steady underlying stochastic process but comparing to the best fixed investment rule. This regret, as we observe, is of the same order of magnitude as that of a Bayesian learner with a continuum prior. However, we show that even such low regret may not be sufficient for survival in asset markets: an agent can have regret as low as $O(\log T)$, but still vanish in market dynamics when competing against agents who invest according to the correct model or even against a perfect Bayesian with a finite prior. On the other hand, we show that Bayesian learning is fragile, while no-regret learning requires less knowledge of the environment and is therefore more robust. Any no-regret learner will drive out of the market an imperfect Bayesian whose finite prior or update rule has even small errors. We formally establish the relationship between notions of survival, vanishing, and market domination studied in economics and the framework of regret minimization, thus bridging these theories.

Stability and Learning in Strategic Queuing Systems

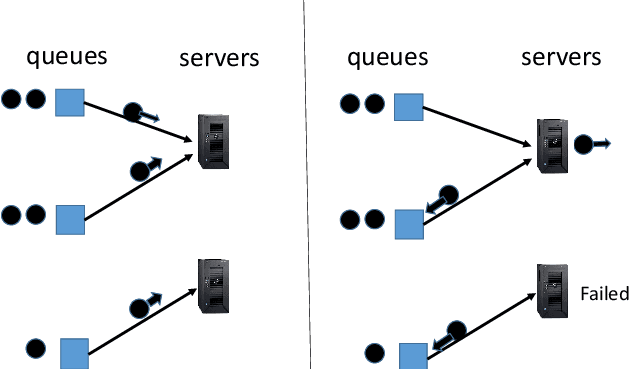
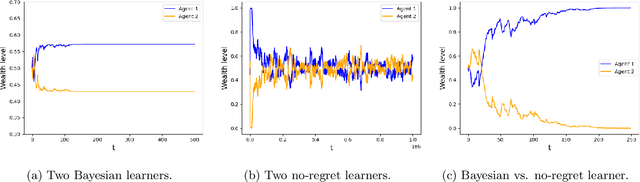
Bounding the price of anarchy, which quantifies the damage to social welfare due to selfish behavior of the participants, has been an important area of research. In this paper, we study this phenomenon in the context of a game modeling queuing systems: routers compete for servers, where packets that do not get service will be resent at future rounds, resulting in a system where the number of packets at each round depends on the success of the routers in the previous rounds. We model this as an (infinitely) repeated game, where the system holds a state (number of packets held by each queue) that arises from the results of the previous round. We assume that routers satisfy the no-regret condition, e.g. they use learning strategies to identify the server where their packets get the best service. Classical work on repeated games makes the strong assumption that the subsequent rounds of the repeated games are independent (beyond the influence on learning from past history). The carryover effect caused by packets remaining in this system makes learning in our context result in a highly dependent random process. We analyze this random process and find that if the capacity of the servers is high enough to allow a centralized and knowledgeable scheduler to get all packets served even with double the packet arrival rate, and queues use no-regret learning algorithms, then the expected number of packets in the queues will remain bounded throughout time, assuming older packets have priority. This paper is the first to study the effect of selfish learning in a queuing system, where the learners compete for resources, but rounds are not all independent: the number of packets to be routed at each round depends on the success of the routers in the previous rounds.

Graph regret bounds for Thompson Sampling and UCB

We study the stochastic multi-armed bandit problem with the graph-based feedback structure introduced by Mannor and Shamir. We analyze the performance of the two most prominent stochastic bandit algorithms, Thompson Sampling and Upper Confidence Bound (UCB), in the graph-based feedback setting. We show that these algorithms achieve regret guarantees that combine the graph structure and the gaps between the means of the arm distributions. Surprisingly this holds despite the fact that these algorithms do not explicitly use the graph structure to select arms. Towards this result we introduce a "layering technique" highlighting the commonalities in the two algorithms.

Small-loss bounds for online learning with partial information

We consider the problem of adversarial (non-stochastic) online learning with partial information feedback, where at each round, a decision maker selects an action from a finite set of alternatives. We develop a black-box approach for such problems where the learner observes as feedback only losses of a subset of the actions that includes the selected action. When losses of actions are non-negative, under the graph-based feedback model introduced by Mannor and Shamir, we offer algorithms that attain the so called "small-loss" $o(\alpha L^{\star})$ regret bounds with high probability, where $\alpha$ is the independence number of the graph, and $L^{\star}$ is the loss of the best action. Prior to our work, there was no data-dependent guarantee for general feedback graphs even for pseudo-regret (without dependence on the number of actions, i.e. utilizing the increased information feedback). Taking advantage of the black-box nature of our technique, we extend our results to many other applications such as semi-bandits (including routing in networks), contextual bandits (even with an infinite comparator class), as well as learning with slowly changing (shifting) comparators. In the special case of classical bandit and semi-bandit problems, we provide optimal small-loss, high-probability guarantees of $\tilde{O}(\sqrt{dL^{\star}})$ for actual regret, where $d$ is the number of actions, answering open questions of Neu. Previous bounds for bandits and semi-bandits were known only for pseudo-regret and only in expectation. We also offer an optimal $\tilde{O}(\sqrt{\kappa L^{\star}})$ regret guarantee for fixed feedback graphs with clique-partition number at most $\kappa$.

Learning in Games: Robustness of Fast Convergence

We show that learning algorithms satisfying a $\textit{low approximate regret}$ property experience fast convergence to approximate optimality in a large class of repeated games. Our property, which simply requires that each learner has small regret compared to a $(1+\epsilon)$-multiplicative approximation to the best action in hindsight, is ubiquitous among learning algorithms; it is satisfied even by the vanilla Hedge forecaster. Our results improve upon recent work of Syrgkanis et al. [SALS15] in a number of ways. We require only that players observe payoffs under other players' realized actions, as opposed to expected payoffs. We further show that convergence occurs with high probability, and show convergence under bandit feedback. Finally, we improve upon the speed of convergence by a factor of $n$, the number of players. Both the scope of settings and the class of algorithms for which our analysis provides fast convergence are considerably broader than in previous work. Our framework applies to dynamic population games via a low approximate regret property for shifting experts. Here we strengthen the results of Lykouris et al. [LST16] in two ways: We allow players to select learning algorithms from a larger class, which includes a minor variant of the basic Hedge algorithm, and we increase the maximum churn in players for which approximate optimality is achieved. In the bandit setting we present a new algorithm which provides a "small loss"-type bound with improved dependence on the number of actions in utility settings, and is both simple and efficient. This result may be of independent interest.

The Price of Anarchy in Auctions

This survey outlines a general and modular theory for proving approximation guarantees for equilibria of auctions in complex settings. This theory complements traditional economic techniques, which generally focus on exact and optimal solutions and are accordingly limited to relatively stylized settings. We highlight three user-friendly analytical tools: smoothness-type inequalities, which immediately yield approximation guarantees for many auction formats of interest in the special case of complete information and deterministic strategies; extension theorems, which extend such guarantees to randomized strategies, no-regret learning outcomes, and incomplete-information settings; and composition theorems, which extend such guarantees from simpler to more complex auctions. Combining these tools yields tight worst-case approximation guarantees for the equilibria of many widely-used auction formats.

No-Regret Learning in Bayesian Games

Recent price-of-anarchy analyses of games of complete information suggest that coarse correlated equilibria, which characterize outcomes resulting from no-regret learning dynamics, have near-optimal welfare. This work provides two main technical results that lift this conclusion to games of incomplete information, a.k.a., Bayesian games. First, near-optimal welfare in Bayesian games follows directly from the smoothness-based proof of near-optimal welfare in the same game when the private information is public. Second, no-regret learning dynamics converge to Bayesian coarse correlated equilibrium in these incomplete information games. These results are enabled by interpretation of a Bayesian game as a stochastic game of complete information.