Learning in Markets with Heterogeneous Agents: Dynamics and Survival of Bayesian vs. No-Regret Learners

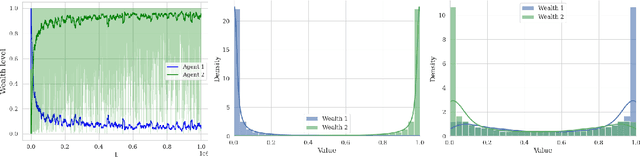
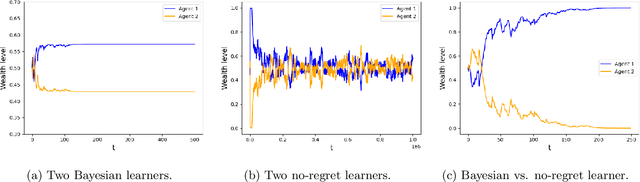
We analyze the performance of heterogeneous learning agents in asset markets with stochastic payoffs. Our agents aim to maximize the expected growth rate of their wealth but have different theories on how to learn this best. We focus on comparing Bayesian and no-regret learners in market dynamics. Bayesian learners with a prior over a finite set of models that assign positive prior probability to the correct model have posterior probabilities that converge exponentially to the correct model. Consequently, they survive even in the presence of agents who invest according to the correct model of the stochastic process. Bayesians with a continuum prior converge to the correct model at a rate of $O((\log T)/T)$. Online learning theory provides no-regret algorithms for maximizing the log of wealth in this setting, achieving a worst-case regret bound of $O(\log T)$ without assuming a steady underlying stochastic process but comparing to the best fixed investment rule. This regret, as we observe, is of the same order of magnitude as that of a Bayesian learner with a continuum prior. However, we show that even such low regret may not be sufficient for survival in asset markets: an agent can have regret as low as $O(\log T)$, but still vanish in market dynamics when competing against agents who invest according to the correct model or even against a perfect Bayesian with a finite prior. On the other hand, we show that Bayesian learning is fragile, while no-regret learning requires less knowledge of the environment and is therefore more robust. Any no-regret learner will drive out of the market an imperfect Bayesian whose finite prior or update rule has even small errors. We formally establish the relationship between notions of survival, vanishing, and market domination studied in economics and the framework of regret minimization, thus bridging these theories.

Constructive Decision Theory

In most contemporary approaches to decision making, a decision problem is described by a sets of states and set of outcomes, and a rich set of acts, which are functions from states to outcomes over which the decision maker (DM) has preferences. Most interesting decision problems, however, do not come with a state space and an outcome space. Indeed, in complex problems it is often far from clear what the state and outcome spaces would be. We present an alternative foundation for decision making, in which the primitive objects of choice are syntactic programs. A representation theorem is proved in the spirit of standard representation theorems, showing that if the DM's preference relation on objects of choice satisfies appropriate axioms, then there exist a set S of states, a set O of outcomes, a way of interpreting the objects of choice as functions from S to O, a probability on S, and a utility function on O, such that the DM prefers choice a to choice b if and only if the expected utility of a is higher than that of b. Thus, the state space and outcome space are subjective, just like the probability and utility; they are not part of the description of the problem. In principle, a modeler can test for SEU behavior without having access to states or outcomes. We illustrate the power of our approach by showing that it can capture decision makers who are subject to framing effects.